сайты для фриланса

 

studwork   Заработок на написании научных работ.  Зарабатывайте на сайте фриланса ежедневно.

биржа ссылок    http://www.rotapost.ru/ 

биржа фриланса https://kwork.ru 

 Биржа консалтинга https://www.liveexpert.ru

Купить хостинг домен    ukraine.com.ua

биржа ссылок рекламы    blogun 

платежная система для фрилансеров capitalist 

Купить книгу " форекс основы " электронная версия, цена 2 доллара

Купить книгу " фото городов США " электронная версия, цена 2 доллара

Купить книгу " 1000 бизнес- идей " электронная версия, цена 2 доллара

Купить книгу "Золотые правила общения" электронная версия, цена 2 доллара

Купить емейл базу 500 000 адресов, пишите на почту

написать по вопросу покупки  

toshatereh@gmail.com   ИЛИ  aarci4772@gmail.com

 Напишите на почту - e - mail,  

Вам дадут реквизиты для оплаты и получите книгу в онлайн формате

 

 

 

Описательная статистика

На этом этапе нам необходимо более подробно рассмотреть основы анализа данных в психологических исследованиях. В этой главе мы сосредоточимся на описательной статистике — наборе методов для обобщения и отображения данных из вашей выборки. Сначала мы рассмотрим некоторые из наиболее распространенных методов описания отдельных переменных, а затем некоторые из наиболее распространенных методов описания статистических взаимосвязей между переменными. Затем мы рассмотрим, как представить описательную статистику в письменной форме, а также в виде таблиц и графиков, которые подходят для исследовательского отчета в стиле Американской психологической ассоциации (АПА). Мы заканчиваем некоторыми практическими советами по организации и проведению ваших анализов.

12.1 Описание отдельных переменных

ЦЕЛИ ОБУЧЕНИЯ

1. Используйте частотные таблицы и гистограммы для отображения и интерпретации распределения переменной.
2. Вычислите и интерпретируйте среднее значение, медиану и моду распределения и определите ситуации, в которых среднее значение, медиана или мода являются наиболее подходящей мерой центральной тенденции.
3. Вычислите и интерпретируйте диапазон и стандартное отклонение распределения.
4. Вычислите и интерпретируйте процентные ранги и z - оценки.

Описательная статистика относится к набору методов обобщения и отображения данных. Предположим здесь, что данные количественные и состоят из баллов по одной или нескольким переменным для каждого из нескольких участников исследования. Хотя в большинстве случаев основной исследовательский вопрос будет касаться одной или нескольких статистических взаимосвязей между переменными, также важно описать каждую переменную в отдельности. По этой причине мы начнем с рассмотрения некоторых наиболее распространенных методов описания одиночных переменных.

Распределение переменной

Каждая переменная имеет распределение , то есть то, как баллы распределяются по уровням этой переменной. Например, в выборке из 100 студентов колледжа распределение переменной «количество братьев и сестер» может быть таким, что 10 из них не имеют братьев и сестер, 30 имеют одного брата и сестру, 40 имеют двух братьев и сестер и так далее. В той же выборке распределение переменной «пол» может быть таким, что 44 человека имеют оценку «мужской», а 56 — «женский».

Таблицы частот

Одним из способов отображения распределения переменной является таблица частот . Таблица 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга», например, представляет собой таблицу частот, показывающую гипотетическое распределение баллов по шкале самооценки Розенберга для выборки из 40 студентов колледжа. В первом столбце перечислены значения переменной — возможные баллы по шкале Розенберга, а во втором — частота каждого балла. Эта таблица показывает, что трое студентов имели самооценку 24 балла, пятеро имели самооценку 23 балла и так далее. Из такой таблицы частот можно быстро увидеть несколько важных аспектов распределения, включая диапазон оценок (от 15 до 24), наиболее и наименее распространенные оценки (22 и 17 соответственно) и любые экстремальные оценки, которые выдерживаются. вне от остальных.

Таблица 12.1 Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга

Самооценка	Частота
24	3
23	5
22	10
21	8
20	5
19	3
18	3
17	0
16	2
15	1

Есть еще несколько моментов, которые стоит отметить в отношении частотных таблиц. Во-первых, уровни, перечисленные в первом столбце, обычно идут от самого высокого вверху к самому низкому внизу, и обычно они не выходят за пределы самых высоких и самых низких оценок в данных. Например, хотя баллы по шкале Розенберга могут варьироваться от 30 до 0, таблица 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга» включает только уровни от 24 до 15, поскольку Диапазон включает все оценки в этом конкретном наборе данных. Во-вторых, при наличии множества различных оценок в широком диапазоне значений часто лучше создать сгруппированную таблицу частот, в которой в первом столбце перечислены диапазоны значений, а во втором — частота оценок в каждом диапазоне.Таблица 12.2 «Сгруппированная таблица частот, показывающая гипотетическое распределение времени реакции» , например, представляет собой сгруппированную таблицу частот, показывающую гипотетическое распределение времени простой реакции для выборки из 20 участников. В сгруппированной таблице частот все диапазоны должны быть одинаковой ширины, и обычно их от пяти до 15. Наконец, частотные таблицы также можно использовать для категориальных переменных, и в этом случае уровни являются метками категорий. Порядок меток категорий несколько произволен, но они часто перечислены от наиболее часто встречающихся вверху до наименее часто встречающихся внизу.

Таблица 12.2 Сгруппированная таблица частот, показывающая гипотетическое распределение времени реакции

Время реакции (мс)	Частота
241–260	1
221–240	2
201–220	2
181–200	9
161–180	4
141–160	2

Гистограммы

Гистограмма — это графическое изображение распределения. В нем представлена ​​та же информация, что и в таблице частот, но в еще более быстром и легком для понимания виде. Гистограмма на рисунке 12.1 «Гистограмма, показывающая распределение баллов самооценки, представленных в» представляет распределение баллов самооценки в таблице 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга» . Ось x гистограммы представляет переменную, а ось y представляет частоту. Над каждым уровнем переменной на x-ось представляет собой вертикальную черту, которая представляет количество людей с этим баллом. Когда переменная является количественной, как в этом примере, между столбцами обычно нет промежутка. Однако когда переменная является категориальной, между ними обычно есть небольшой разрыв. (Разрыв в 17 на этой гистограмме отражает тот факт, что в этом наборе данных не было 17 баллов.)

Рисунок 12.1 Гистограмма, показывающая распределение баллов самооценки, представленное в таблице 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга»

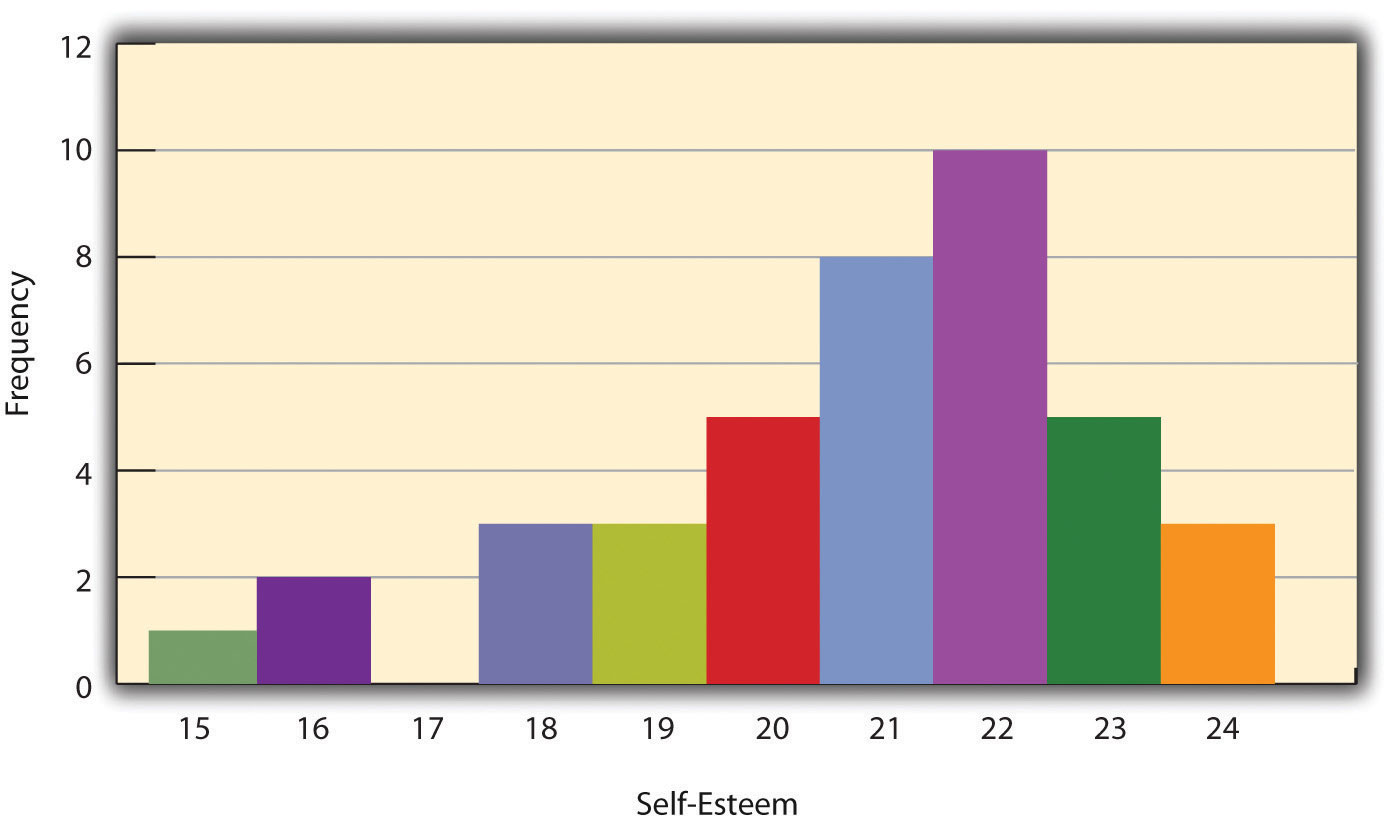
Формы распределения

Когда распределение количественной переменной отображается на гистограмме, оно имеет форму. Типична форма распределения оценок самооценки на рис. 12.1 «Гистограмма, показывающая распределение оценок самооценки, представленных на» . Есть пик где-то около середины распределения и «хвосты», которые сужаются в любом направлении от пика. Распределение на рис. 12.1 «Гистограмма, показывающая распределение показателей самооценки, представленное в » является унимодальным, то есть имеет один отчетливый пик, но распределения также могут быть бимодальными, то есть они имеют два отчетливых пика. Рисунок 12.2 «Гистограмма, показывающая гипотетическое бимодальное распределение баллов по шкале депрессии Бека», например, показывает гипотетическое бимодальное распределение баллов по опроснику депрессии Бека. Распределения также могут иметь более двух отчетливых пиков, но в психологических исследованиях они встречаются относительно редко.

Рисунок 12.2. Гистограмма, показывающая гипотетическое бимодальное распределение баллов по шкале депрессии Бека.

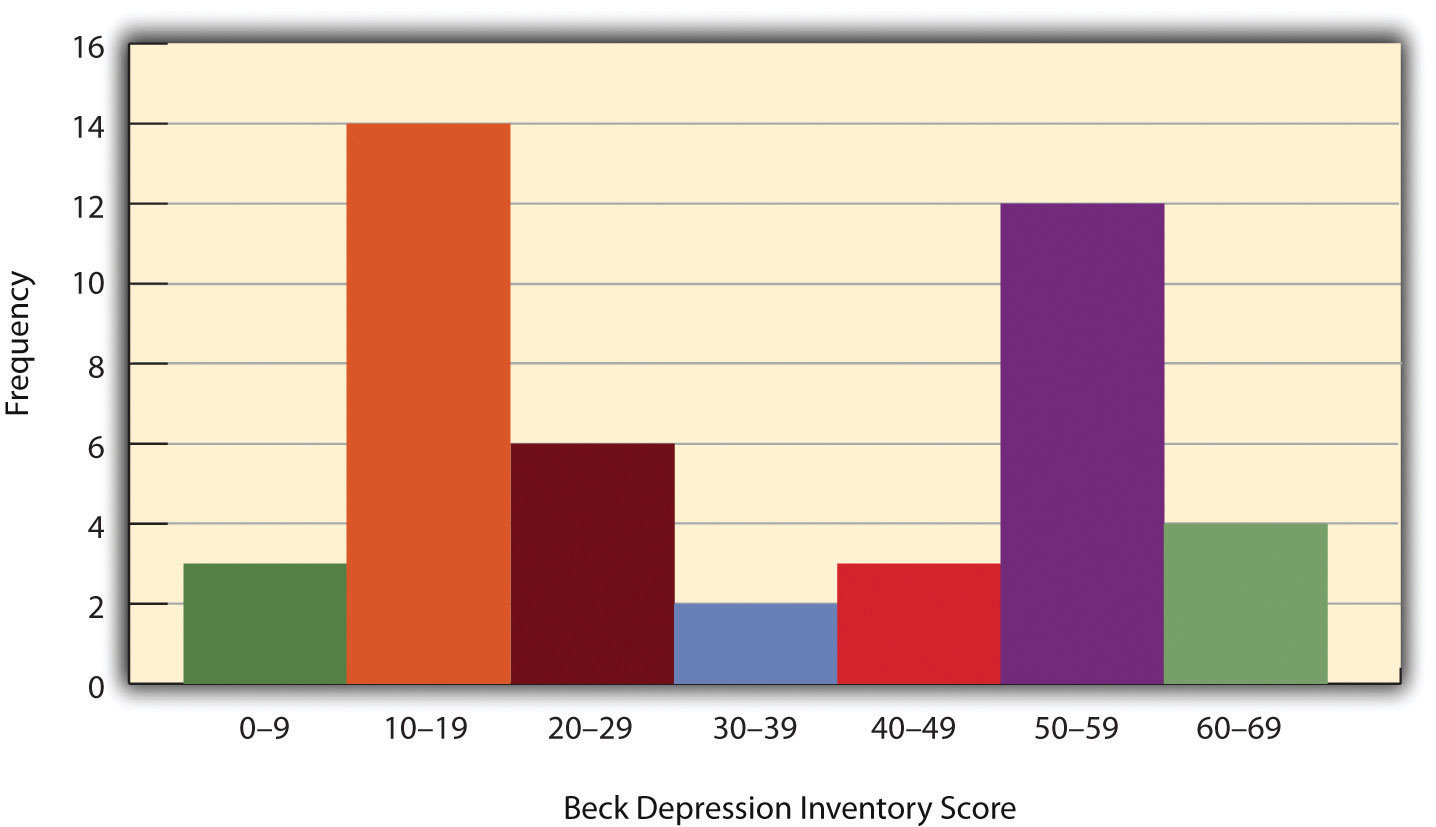
Другой характеристикой формы распределения является то, является ли оно симметричным или асимметричным. Распределение в центре рисунка 12.3 «Гистограммы, показывающие распределение с отрицательным, симметричным и положительным смещением» является симметричным . Его левая и правая половины являются зеркальным отражением друг друга. Распределение слева имеет отрицательную асимметрию , его пик смещен к верхней границе диапазона и относительно длинный отрицательный хвост. Распределение справа имеет положительную асимметрию с пиком в нижней части диапазона и относительно длинным положительным хвостом.

Рисунок 12.3 . Гистограммы, показывающие распределения с отрицательным, симметричным и положительным наклоном

Выброс — это крайняя оценка, которая намного выше или ниже остальных оценок в распределении. Иногда выбросы представляют собой действительно экстремальные значения интересующей нас переменной. Например, в опроснике депрессии Бека один человек с клинической депрессией может быть исключением в выборке счастливых и хорошо функционирующих сверстников. Однако выбросы могут также указывать на ошибки или непонимание со стороны исследователя или участника, неисправности оборудования или аналогичные проблемы. Подробнее о том, как интерпретировать выбросы и что с ними делать, мы поговорим позже в этой главе.

Меры центральной тенденции и изменчивости

Также полезно иметь возможность более точно описать характеристики распределения. Здесь мы рассмотрим, как это сделать с точки зрения двух важных характеристик: их центральной тенденции и их изменчивости.

Главная тенденция

Центральной тенденцией распределения является его середина — точка, вокруг которой имеют тенденцию группироваться оценки в распределении. (Другой термин для обозначения центральной тенденции — средняя .) Оглядываясь назад на рисунок 12.1 «Гистограмма, показывающая распределение показателей самооценки, представленных в» , например, мы можем видеть, что показатели самооценки имеют тенденцию концентрироваться вокруг значений от 20 до 22. Здесь мы рассмотрим три наиболее распространенных показателя центральной тенденции: среднее значение, медиану и моду.

Среднее значение распределения (обозначается символом M ) представляет собой сумму баллов, деленную на количество баллов. В виде формулы это выглядит так:

В этой формуле символ Σ (греческая буква сигма) является знаком суммирования и означает суммирование значений переменной X . N представляет количество баллов. Среднее значение, безусловно, является наиболее распространенным показателем центральной тенденции, и для этого есть несколько веских причин. Обычно он дает хорошее представление о центральной тенденции распределения и легко понятен большинству людей. Кроме того, среднее значение имеет статистические свойства, которые делают его особенно полезным при выводе статистики.

Альтернативой среднему является медиана. Медиана — это средний балл в том смысле, что половина баллов в распределении меньше его, а половина больше его. Самый простой способ найти медиану — упорядочить оценки от низших к высшим и расположить оценку посередине. Рассмотрим, например, следующий набор из семи баллов:

8 4 12 14 3 2 3

Чтобы найти медиану, просто переставьте баллы от самого низкого к самому высокому и найдите тот, который находится посередине.

2 3 3 4 8 12 14

В этом случае медиана равна 4, потому что есть три балла ниже 4 и три балла выше 4. Когда имеется четное количество баллов, в середине распределения находятся два балла, и в этом случае медиана является значение на полпути между ними. Например, если бы мы добавили к предыдущему набору данных оценку 15, в середине распределения оказались бы две оценки (обе 4 и 8), а медиана оказалась бы посередине между ними (6).

Последним показателем центральной тенденции является мода. Мода — это наиболее часто встречающаяся оценка в распределении. В распределении самооценки, представленном в таблице 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга» и на рисунке 12.1 «Гистограмма, показывающая распределение баллов самооценки, представленных в » , например, режим 22. Такой балл был у большего числа студентов, чем любой другой. Мода — это единственная мера центральной тенденции, которую также можно использовать для категориальных переменных.

В одномодальном и симметричном распределении среднее значение, медиана и мода будут очень близки друг к другу на пике распределения. В бимодальном или асимметричном распределении среднее значение, медиана и мода могут быть совершенно разными. В бимодальном распределении среднее значение и медиана будут находиться между пиками, а мода будет находиться на самом высоком пике. В асимметричном распределении среднее значение будет отличаться от медианы в направлении асимметрии (т. е. в направлении более длинного хвоста). Для распределений с большой асимметрией среднее значение может быть сдвинуто настолько далеко в направлении асимметрии, что оно уже не является хорошей мерой центральной тенденции этого распределения. Представьте, например, набор из четырех простых времен реакции: 200, 250, 280 и 250 миллисекунд (мс). Среднее значение составляет 245 мс. Но добавление еще одной оценки 5, 000 мс — возможно, потому, что участник не обращал внимания — увеличило бы среднее значение до 1445 мс. Мало того, что эта мера центральной тенденции превышает 80% баллов в распределении, она также, по-видимому, не очень хорошо отражает поведение кого-либо в распределении. Вот почему исследователи часто предпочитают медиану для сильно асимметричных распределений (таких как распределения времени реакции).

Однако имейте в виду, что при анализе данных вам не обязательно выбирать единственную меру центральной тенденции. Каждый из них предоставляет немного разную информацию, и все они могут быть полезны.

Меры изменчивости

Изменчивость распределения — это степень, в которой оценки варьируются вокруг своей центральной тенденции. Рассмотрим два распределения на рис. 12.4 «Гистограммы, показывающие гипотетические распределения с одним и тем же средним значением, медианой и модой (10), но с низкой изменчивостью (вверху) и высокой изменчивостью (внизу)» , оба из которых имеют одну и ту же центральную тенденцию. Среднее значение, медиана и мода каждого распределения равны 10. Обратите внимание, однако, что эти два распределения различаются с точки зрения их изменчивости. Верхний имеет относительно низкую изменчивость, все оценки относительно близки к центру. Нижний имеет относительно высокую изменчивость, а оценки разбросаны по гораздо большему диапазону.

Рис. 12.4 . Гистограммы, показывающие гипотетические распределения с одинаковыми средним значением, медианой и модой (10), но с низкой вариабельностью (вверху) и высокой вариабельностью (внизу)

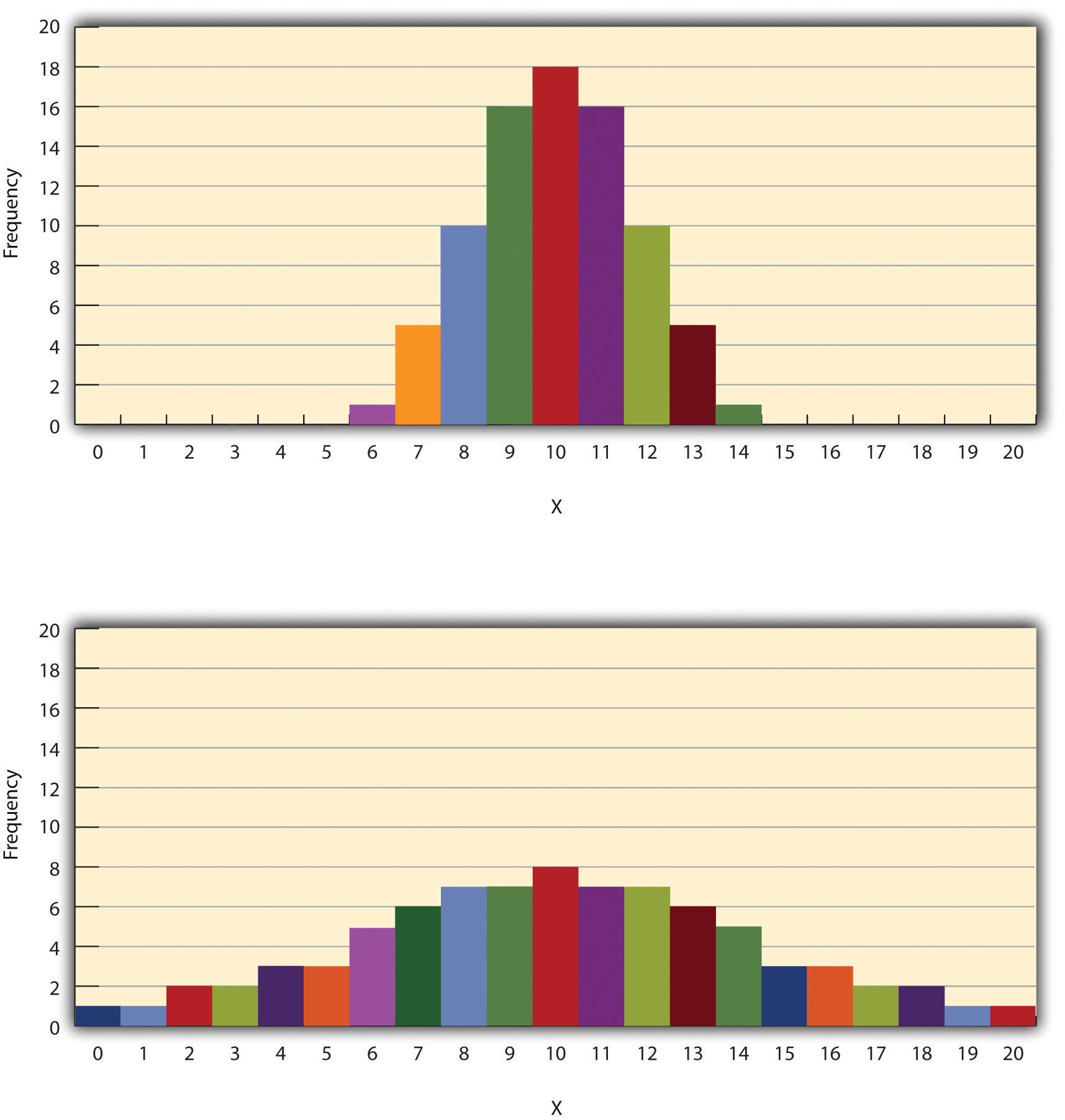
Одной из простых мер изменчивости является диапазон , который представляет собой просто разницу между наивысшим и наименьшим баллами в распределении. Диапазон значений самооценки в таблице 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга», например, представляет собой разницу между самым высоким баллом (24) и самым низким баллом (15). То есть диапазон равен 24 − 15 = 9. Хотя диапазон легко вычислить и понять, он может ввести в заблуждение, когда есть выбросы. Представьте себе, например, экзамен, на котором все студенты набрали от 90 до 100 баллов. Он имеет диапазон 10. Но если бы был один студент, набравший 20 баллов, диапазон увеличился бы до 80, создавая впечатление, что баллы были одинаковыми. весьма различны, когда на самом деле только один ученик существенно отличался от остальных.

Безусловно, наиболее распространенной мерой изменчивости является стандартное отклонение. Стандартное отклонение распределения — это, грубо говоря, среднее расстояние между оценками и средним значением. Например, стандартные отклонения распределений на рис. 12.4 «Гистограммы, показывающие гипотетические распределения с одинаковыми средним значением, медианой и модой (10), но с низкой изменчивостью (вверху) и высокой изменчивостью (внизу)» составляют 1,69 для верхнего распределения и 4.30 для нижнего. То есть, в то время как баллы в верхнем распределении отличаются от среднего примерно на 1,69 единицы в среднем, баллы в нижнем распределении отличаются от среднего примерно на 4,30 единицы в среднем.

Вычисление стандартного отклонения связано с небольшой сложностью. В частности, он включает в себя нахождение разницы между каждой оценкой и средним значением, возведение каждой разницы в квадрат, нахождение среднего значения этих квадратов разностей и, наконец, нахождение квадратного корня из этого среднего значения. Формула выглядит следующим образом:

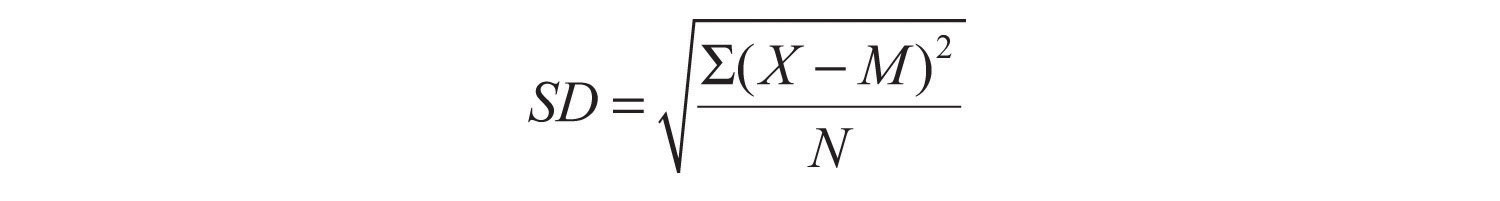
Вычисления стандартного отклонения проиллюстрированы для небольшого набора данных в таблице 12.3 «Вычисления стандартного отклонения» . Первый столбец представляет собой набор из восьми оценок со средним значением 5. Второй столбец представляет собой разницу между каждой оценкой и средним значением. Третий столбец представляет собой квадрат каждой из этих разностей. Обратите внимание, что хотя различия могут быть отрицательными, квадраты различий всегда положительны, а это означает, что стандартное отклонение всегда положительно. В нижней части третьего столбца находится среднее значение квадратов разностей, которое также называется дисперсией (обозначается как SD ^{2 ).}). Хотя дисперсия сама по себе является мерой изменчивости, она обычно играет большую роль в выводной статистике, чем в описательной статистике. Наконец, под дисперсией находится квадратный корень из дисперсии, который является стандартным отклонением.

Таблица 12.3 Расчеты стандартного отклонения

Икс	Х – М	( Икс - М ) 2
3	−2	4
5	0	0
4	−1	1
2	−3	9
7	2	4
6	1	1
5	0	0
8	3	9
М = 5

N или N - 1

Если вы уже прошли курс статистики, вы, возможно, научились делить сумму квадратов разностей на N - 1, а не на N , когда вычисляете дисперсию и стандартное отклонение. Почему это?

По определению стандартное отклонение представляет собой квадратный корень из среднего значения квадратов разностей. Это подразумевает деление суммы квадратов разностей на N , как в только что представленной формуле. Вычисление стандартного отклонения таким образом уместно, когда ваша цель состоит в том, чтобы просто описать изменчивость в образце. И изучение этого таким образом подчеркивает, что дисперсия на самом деле является средним значением квадратов разностей, а стандартное отклонение — это квадратный корень из этого среднего .

Однако большинство калькуляторов и пакетов программного обеспечения делят сумму квадратов разностей на N - 1. Это связано с тем, что стандартное отклонение выборки имеет тенденцию быть немного ниже, чем стандартное отклонение совокупности, из которой была выбрана выборка. Деление суммы квадратов на N − 1 корректирует эту тенденцию и дает более точную оценку стандартного отклонения генеральной совокупности. Поскольку исследователи обычно думают о своих данных как о выборке, отобранной из большей совокупности, и поскольку они, как правило, заинтересованы в выводах о населении, имеет смысл регулярно применять эту поправку.

Процентильные ранги и z - оценки

Во многих ситуациях полезно иметь способ описать положение отдельной оценки в ее распределении. Одним из подходов является процентильный ранг. Процентильный ранг оценки — это процент оценок в распределении, которые ниже этой оценки. Рассмотрим, например, распределение в таблице 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга» . Для любой оценки в распределении мы можем найти ее процентильный ранг, подсчитав количество оценок в распределении, которые ниже этой оценки, и преобразовав это число в процент от общего количества оценок. Обратите внимание, например, что пять студентов, представленных данными вВ Таблице 12.1 «Таблица частот, показывающая гипотетическое распределение баллов по шкале самооценки Розенберга» самооценка равнялась 23 баллам. В этом распределении 32 из 40 баллов (80%) ниже 23. Таким образом, каждый из этих студентов имеет процентильный ранг 80. (Можно также сказать, что они набрали «80-й процентиль».) Процентильные ранги часто используются для сообщения результатов стандартизированных тестов способностей или достижений. Например, если ваш процентильный ранг в тесте на вербальные способности равен 40, это будет означать, что вы набрали больше, чем 40% людей, прошедших тест.

Другой подход — оценка z . Оценка z для конкретного человека представляет собой разницу между оценкой этого человека и средним значением распределения, деленную на стандартное отклонение распределения :

Показатель z указывает, насколько выше или ниже среднего находится необработанный показатель, но он выражает это в терминах стандартного отклонения. Например, при распределении оценок коэффициента интеллекта (IQ) со средним значением 100 и стандартным отклонением 15 показатель IQ 110 будет иметь z -показатель (110 - 100) / 15 = +0,67. Другими словами, оценка 110 на 0,67 стандартного отклонения (примерно две трети стандартного отклонения) выше среднего. Точно так же исходная оценка 85 будет иметь z -оценку (85 - 100) / 15 = -1,00. Другими словами, 85 баллов — это одно стандартное отклонение ниже среднего.

Есть несколько причин, по которым z -показатели важны. Опять же, они обеспечивают способ описания того, где находится индивидуальный балл в распределении, и иногда используются для сообщения результатов стандартизированных тестов. Они также обеспечивают один из способов определения выбросов. Например, выбросы иногда определяются как оценки, у которых z -оценка меньше -3,00 или больше +3,00. Другими словами, они определяются как баллы, которые более чем на три стандартных отклонения от среднего значения. Наконец, z -показатели играют важную роль в понимании и вычислении других статистических данных, как мы вскоре увидим.

Описательная онлайн-статистика

Хотя многие исследователи используют коммерчески доступное программное обеспечение, такое как SPSS и Excel, для анализа своих данных, существует несколько бесплатных онлайн-инструментов для анализа, которые также могут быть чрезвычайно полезными. Многие позволяют вам вводить или загружать свои данные, а затем одним щелчком мыши проводить несколько описательных статистических анализов. Среди них следующие.

Виртуальная лаборатория риса по статистике

http://onlinestatbook.com/stat_analysis/index.html

VassarStats

http://faculty.vassar.edu/lowry/VassarStats.html

Яркий стат

http://www.brightstat.com

Более полный список см . на http://statpages.org/index.html .

КЛЮЧЕВЫЕ ВЫВОДЫ

• Каждая переменная имеет распределение — способ распределения оценок по уровням. Распределение можно описать с помощью таблицы частот и гистограммы. Его также можно описать словами с точки зрения его формы, в том числе, является ли он одномодальным или бимодальным, а также является ли он симметричным или перекошенным.
• Центральную тенденцию, или середину, распределения можно точно описать с помощью трех статистик — среднего, медианы и моды. Среднее значение представляет собой сумму баллов, деленную на количество баллов, медиана — это средний балл, а мода — это наиболее распространенный балл.
• Изменчивость или разброс распределения можно точно описать с помощью диапазона и стандартного отклонения. Диапазон — это разница между самой высокой и самой низкой оценкой, а стандартное отклонение — это примерно средняя величина, на которую оценки отличаются от среднего.
• Расположение оценки в ее распределении можно описать с помощью процентилей или z - оценок. Процентиль оценки — это процент оценок ниже этой оценки, а z - оценка — это разница между оценкой и средним значением, деленная на стандартное отклонение.

УПРАЖНЕНИЯ

1. Практика: Составьте частотную таблицу и гистограмму для следующих данных. Затем напишите краткое описание формы распределения словами.

   11, 8, 9, 12, 9, 10, 12, 13, 11, 13, 12, 6, 10, 17, 13, 11, 12, 12, 14, 14

2. Практика. Для данных в упражнении 1 вычислите среднее значение, медиану, моду, стандартное отклонение и диапазон.
3. Практика: используя данные из упражнений 1 и 2, найдите (а) процентные ранги для оценок 9 и 14 и (б) z - значения для оценок 8 и 12.

12.2 Описание статистических взаимосвязей

ЦЕЛИ ОБУЧЕНИЯ

1. Опишите различия между группами с точки зрения их средних значений и стандартных отклонений, а также с точки зрения d Коэна .
2. Опишите корреляции между количественными переменными в терминах r Пирсона .

Как мы видели на протяжении всей этой книги, самые интересные исследовательские вопросы в психологии связаны со статистическими отношениями между переменными. Напомним, что существует статистическая связь между двумя переменными, когда средний балл по одной систематически различается по уровням другой. В этом разделе мы вернемся к двум основным формам статистических отношений, представленным ранее в книге, — различиям между группами или условиями и отношениям между количественными переменными — и рассмотрим, как их описать более подробно.

Различия между группами или условиями

Различия между группами или состояниями обычно описываются в терминах среднего значения и стандартного отклонения для каждой группы или состояния. Например, Томас Оллендик и его коллеги провели исследование, в котором оценили два однократных лечения простых фобий у детей (Ollendick et al., 2009). Оллендик, Т. Х., Ост, Л.-Г., Рейтершельд, Л., Коста, Н., Седерлунд, Р., Сирбу, К.,… Джарретт, Массачусетс (2009). Лечение специфических фобий у молодежи за один сеанс: рандомизированное клиническое исследование в США и Швеции. Журнал консалтинга и клинической психологии, 77 , 504–516.Они случайным образом распределяли детей с сильным страхом (например, перед собаками) в одно из трех состояний. В условиях воздействия дети фактически столкнулись с объектом своего страха под руководством обученного терапевта. В условиях обучения они узнали о фобиях и некоторых стратегиях борьбы с ними. В контрольном состоянии списка ожидания они ожидали лечения после завершения исследования. Тяжесть фобии каждого ребенка затем оценивалась по шкале от 1 до 8 врачом, который не знал, какое лечение получал ребенок. (Это была одна из нескольких зависимых переменных.) Средняя оценка страха в условиях обучения составила 4,83 при стандартном отклонении 1,52, в то время как средняя оценка страха в условиях воздействия составила 3,47 при стандартном отклонении 1,77. Средняя оценка страха в контрольном состоянии составила 5. 56 со стандартным отклонением 1,21. Другими словами, оба метода лечения работали, но метод воздействия работал лучше, чем метод обучения. Как мы видели, различия между средними группами или условиями могут быть представлены в виде гистограммы, подобной приведенной вРисунок 12.5 «Гистограмма, показывающая средние оценки фобии клиницистов для детей в двух условиях лечения» , где высота столбцов представляет средние значения для группы или состояния. Вскоре мы более подробно рассмотрим создание гистограмм в стиле Американской психологической ассоциации (АПА).

Рис. 12.5 Гистограмма, показывающая средние оценки фобии клиницистов для детей в двух условиях лечения

Также важно уметь описывать силу статистической зависимости, которую часто называют величиной эффекта . Наиболее широко используемая мера размера эффекта для различий между средними группами или состояниями называется d Коэна , которая представляет собой разницу между двумя средними значениями, деленную на стандартное отклонение:

$$$$

В этой формуле не имеет большого значения, какое среднее значение равно M ₁ , а какое — M ₂ . Если есть группа лечения и контрольная группа, среднее значение группы лечения обычно равно М ₁ , а среднее значение контрольной группы равно М ₂ . В противном случае большее среднее обычно равно M ₁ , а меньшее среднее M _{2 , так что} d Коэнаоказывается положительным. Стандартное отклонение в этой формуле обычно представляет собой своего рода среднее значение двух групповых стандартных отклонений, называемое стандартным отклонением объединенных групп. Чтобы вычислить объединенное стандартное отклонение внутри групп, добавьте сумму квадратов различий для группы 1 к сумме квадратов различий для группы 2, разделите это на сумму двух размеров выборки, а затем извлеките из нее квадратный корень. Однако неформально вместо этого можно использовать стандартное отклонение любой группы.

Концептуально d Коэна представляет собой разницу между двумя средними значениями, выраженную в единицах стандартного отклонения. (Обратите внимание на его сходство с оценкой z , которая выражает разницу между индивидуальной оценкой и средним значением в единицах стандартного отклонения.) Значение d Коэна, равное 0,50, означает, что средние значения двух групп отличаются на 0,50 стандартных отклонений (половина стандартного отклонения). Коэффициент Коэна, равный 1,20, означает, что они отличаются на 1,20 стандартных отклонения. Но как мы должны интерпретировать эти значения с точки зрения силы связи или размера разницы между средними значениями? В таблице 12.4 «Рекомендации по обращению к Коэну» представлены некоторые рекомендации по интерпретации d Коэна.ценности в психологических исследованиях (Cohen, 1992). Коэн, Дж. (1992). Силовой праймер. Психологический бюллетень, 112 , 155–159. Значения около 0,20 считаются малыми, значения около 0,50 считаются средними, а значения около 0,80 считаются большими. Таким образом, значение d Коэна, равное 0,50, представляет собой среднюю разницу между двумя средними значениями, а значение d Коэна, равное 1,20, представляет собой очень большую разницу в контексте психологических исследований. В исследовании Оллендика и его коллег наблюдалась большая разница ( d = 0,82) между условиями воздействия и образования.

Таблица 12.4 Рекомендации по использованию значений Коэна d и Пирсона r как «сильных», «средних» или «слабых»

Сила отношений	Коэн д	Пирсон р
Сильный/большой	± 0,80	± 0,50
Середина	± 0,50	± 0,30
Слабый/маленький	± 0,20	± 0,10

Коэффициент d Коэна полезен, потому что он имеет одно и то же значение независимо от сравниваемой переменной или шкалы, по которой она была измерена. Коэффициент Коэна, равный 0,20, означает, что средние значения двух групп отличаются на 0,20 стандартных отклонений, независимо от того, говорим ли мы об оценках по шкале самооценки Розенберга, времени реакции, измеренном в миллисекундах, количестве братьев и сестер или диастолическом артериальном давлении, измеренном в миллиметрах ртутного столба. Это не только облегчает исследователям обмен информацией друг с другом о своих результатах, но также позволяет комбинировать и сравнивать результаты разных исследований с использованием разных показателей.

Имейте в виду, что термин « величина эффекта » может ввести в заблуждение, поскольку предполагает наличие причинно-следственной связи — что разница между двумя средними значениями является «эффектом» пребывания в одной группе или состоянии, а не в другом. Представьте себе, например, исследование, показывающее, что группа занимающихся спортом в среднем счастливее, чем группа не занимающихся спортом, с «величиной эффекта» d .= 0,35. Если бы исследование было экспериментом — с участниками, случайным образом распределенными в условия упражнений и без упражнений, — тогда можно было бы сделать вывод, что упражнения вызывали небольшое или среднее увеличение счастья. Однако если бы исследование было корреляционным, то можно было бы сделать вывод только о том, что тренирующиеся были счастливее тех, кто не тренировался, на небольшую или среднюю величину. Другими словами, простое определение разницы как «величины эффекта» не делает связь причинно-следственной.

Половые различия, выраженные как Коэнов d

Исследователь Джанет Шибли Хайд изучила результаты многочисленных исследований психологических половых различий и выразила их в терминах d Коэна (Hyde, 2007). Хайд, Дж. С. (2007). Новые направления в изучении гендерных сходств и различий. Текущие направления в психологической науке, 16 , 259–263. Ниже приведены некоторые значения, которые она нашла, усредненные по нескольким исследованиям в каждом случае. (Обратите внимание, что поскольку она всегда рассматривает среднее значение для мужчин как M ₁ , а среднее значение для женщин как M ₂ , положительные значения указывают на то, что мужчины набирают более высокие баллы, а отрицательные значения указывают на то, что женщины набирают более высокие баллы.)

Решение математических задач	+0,08
Понимание прочитанного	−0,09
Улыбается	−0,40
Агрессия	+0,50
Отношение к случайному сексу	+0,81
Эффективность лидерства	−0,02

Хайд указывает, что, хотя мужчины и женщины сильно различаются по некоторым переменным (например, по отношению к случайным половым связям), они отличаются лишь незначительно по подавляющему большинству. Во многих случаях d Коэна меньше 0,10, что она называет «тривиальной» разницей. (Различие в разговорчивости, обсуждавшееся в главе 1 «Психологическая наука» , также было тривиальным: d = 0,06.) Хотя как исследователи, так и неисследователи часто подчеркивают половые различия , Хайд утверждал, что не менее разумно думать о мужчинах и женщины принципиально похожи . Она называет это «гипотезой гендерного сходства».

Корреляции между количественными переменными

Как мы видели на протяжении всей книги, многие интересные статистические взаимосвязи принимают форму корреляций между количественными переменными. Например, исследователи Курт Карлсон и Жаклин Конард провели исследование взаимосвязи между алфавитным положением первой буквы фамилий людей (от A = 1 до Z = 26) и тем, насколько быстро эти люди реагировали на призывы потребителей (Carlson & Conard). , 2011). Карлсон, К.А., и Конард, Дж.М. (2011). Эффект фамилии: как фамилия влияет на время приобретения. Журнал потребительских исследований . дои: 10.1086/658470В одном исследовании они разослали электронные письма большой группе студентов MBA, предлагая бесплатные билеты на баскетбол из ограниченного количества. В результате, чем ближе к концу алфавита стояли фамилии студентов, тем быстрее они отвечали. Эти результаты обобщены на рис. 12.7 «Линейный график, показывающий взаимосвязь между расположением фамилий людей в алфавитном порядке и тем, насколько быстро эти люди реагируют на предложения потребительских товаров» .

Рис. 12.7 Линейный график, показывающий взаимосвязь между расположением фамилий людей в алфавитном порядке и тем, насколько быстро эти люди реагируют на предложения потребительских товаров

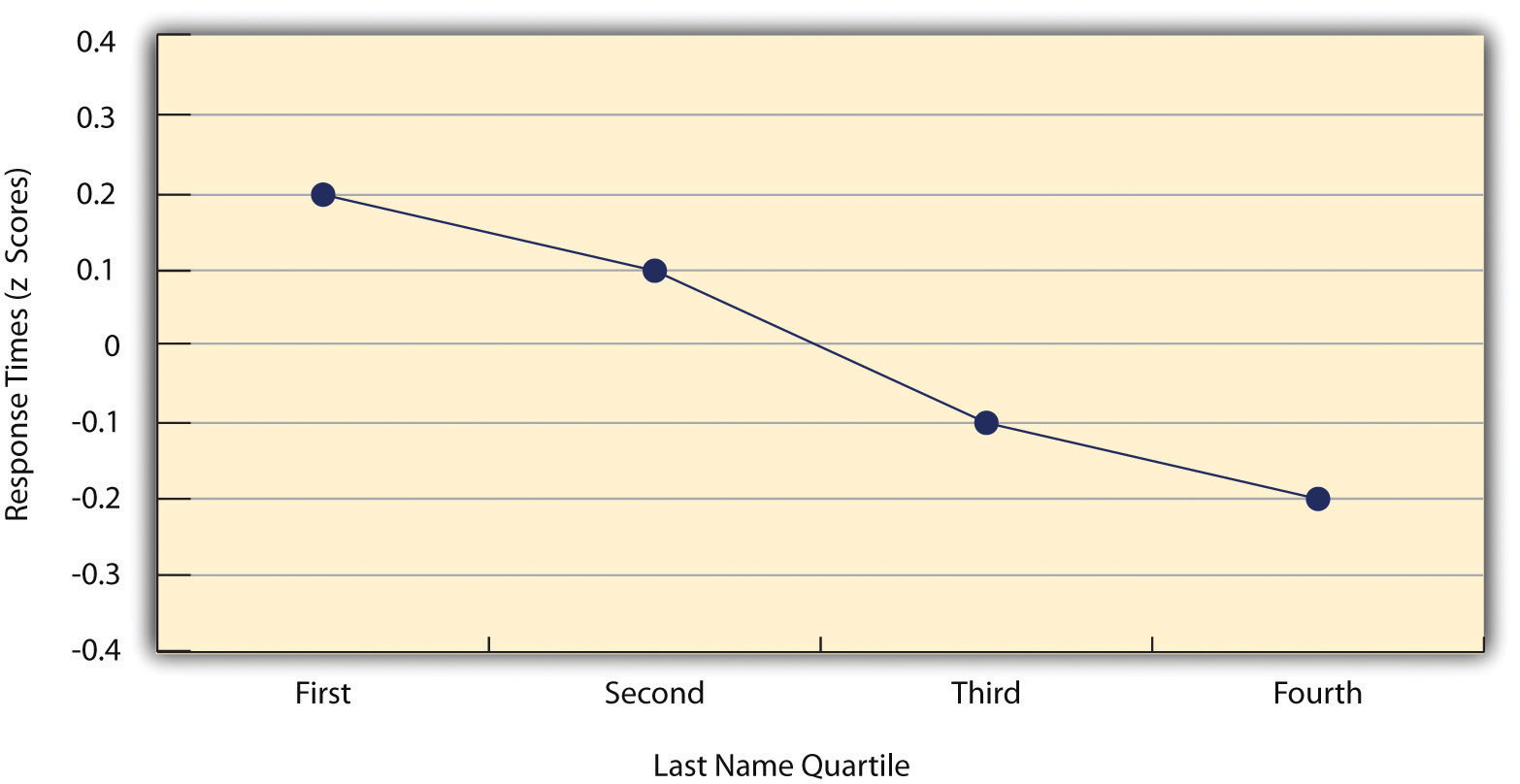
Такие отношения часто представляются с помощью линейных графиков или диаграмм рассеяния, которые показывают, как уровень одной переменной различается в диапазоне другой. Например, на линейном графике на рис. 12.7 «Линейный график, показывающий взаимосвязь между расположением фамилий людей в алфавитном порядке и тем, как быстро эти люди реагируют на предложения потребительских товаров» , каждая точка представляет среднее время отклика для участников с фамилиями в первый, второй, третий и четвертый квартили (или четверти) распределения имен. Это ясно показывает, как время отклика имеет тенденцию к снижению по мере приближения фамилий людей к концу алфавита. Диаграмма рассеяния вНа рис. 12.8 «Статистическая взаимосвязь между оценками нескольких студентов колледжа по шкале самооценки Розенберга, полученной два раза с разницей в неделю» , воспроизведенной из главы 5 «Психологические измерения» , показана взаимосвязь между оценками студентов по 25 методам исследования по шкале самооценки Розенберга. Шкала самооценки Розенберга проводится два раза с интервалом в неделю. Здесь баллы представляют отдельных лиц, и мы можем видеть, что чем выше учащиеся набрали баллы в первый раз, тем выше они, как правило, набирали баллы во второй раз. Как правило, линейные графики используются, когда переменная на оси x имеет (или организована) небольшое количество различных значений, таких как четыре квартили распределения имен. Диаграммы рассеяния используются, когда переменная на x-ось имеет большое количество значений, таких как различные возможные оценки самооценки.

Рис. 12.8 Статистическая зависимость между оценками нескольких студентов колледжа по шкале самооценки Розенберга, полученной два раза с разницей в неделю

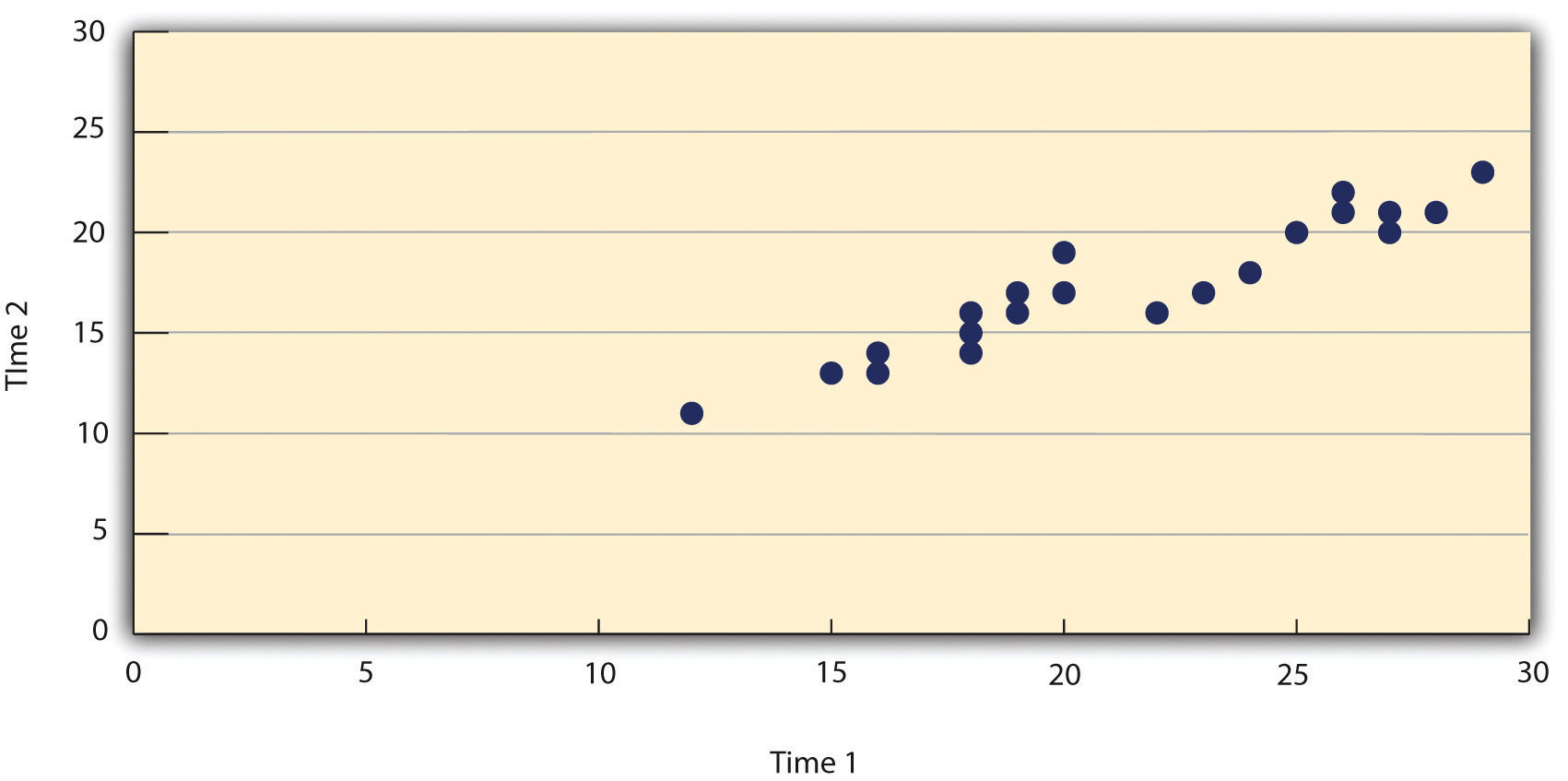
Данные, представленные на рис. 12.8 «Статистическая взаимосвязь между оценками нескольких студентов колледжа по шкале самооценки Розенберга, полученными два раза с интервалом в неделю» , представляют собой хороший пример положительной взаимосвязи, при которой более высокие баллы по одной переменной, как правило, связаны с более высокими баллами по другому (так, чтобы точки шли из левого нижнего угла в правый верхний угол графика). Данные, представленные на рис. 12.7 «Линейный график, показывающий взаимосвязь между расположением фамилий людей в алфавитном порядке и тем, насколько быстро эти люди реагируют на предложения потребительских товаров» , представляют собой хороший пример отрицательной взаимосвязи.

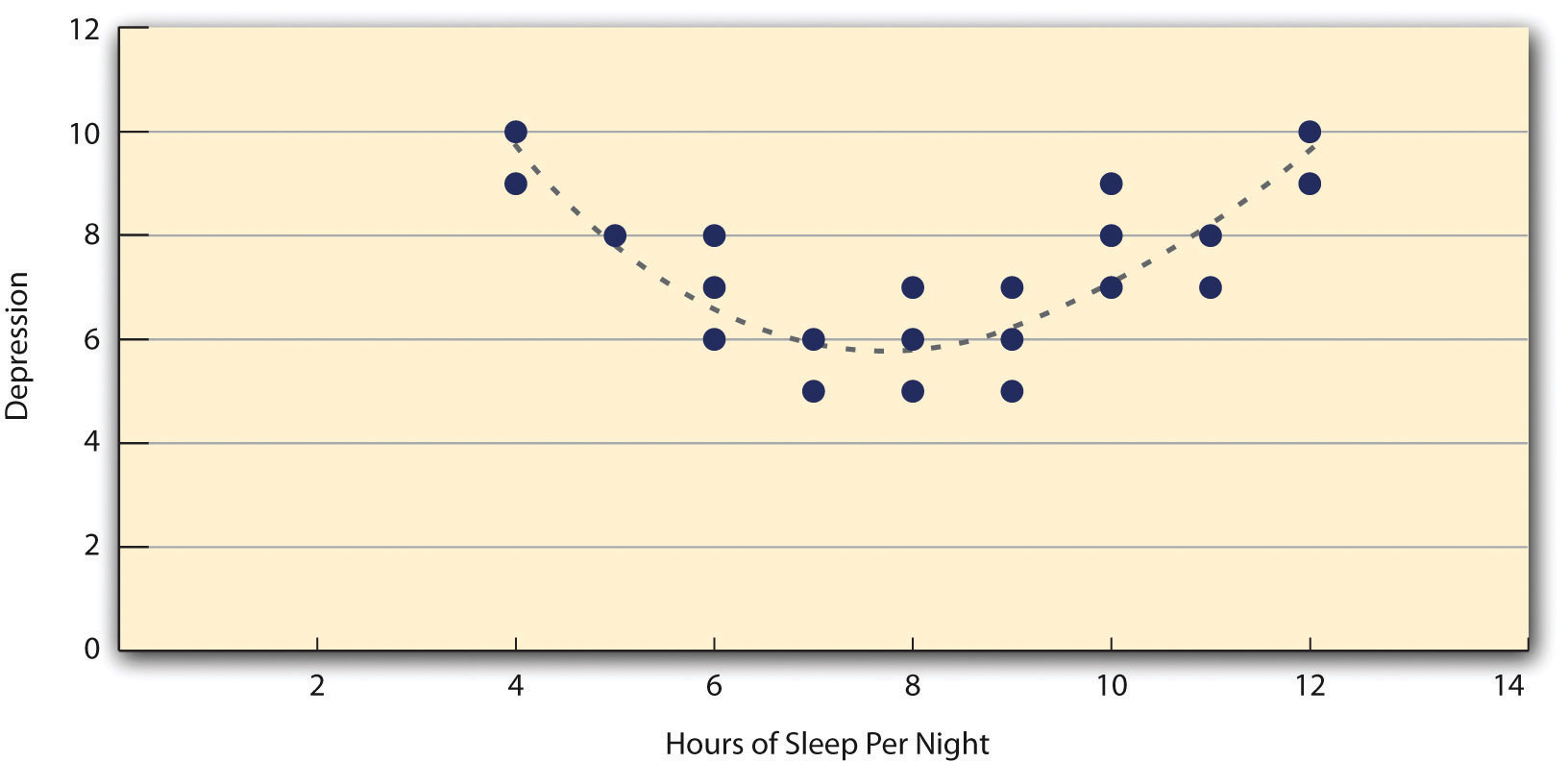
Оба этих примера также являются линейными отношениями, в которых точки достаточно хорошо укладываются одной прямой линией. Нелинейные отношения — это отношения, в которых точки лучше соответствуют изогнутой линии. Рисунок 12.9 «Гипотетическая нелинейная зависимость между тем, сколько человек спит за ночь, и тем, насколько они подавлены», например, показывает гипотетическую связь между количеством сна, которое люди получают за ночь, и уровнем их депрессии. В этом примере линия, которая лучше всего соответствует точкам, представляет собой кривую — своего рода перевернутую букву «U», потому что люди, которые спят около восьми часов, как правило, менее всего подвержены депрессии, в то время как те, кто спит слишком мало, и те, кто слишком много сна, как правило, более депрессии. Нелинейные отношения не редкость в психологии, но их подробное обсуждение выходит за рамки этой книги.

Рис. 12.9 . Гипотетическая нелинейная зависимость между тем, сколько человек спит за ночь, и степенью депрессии

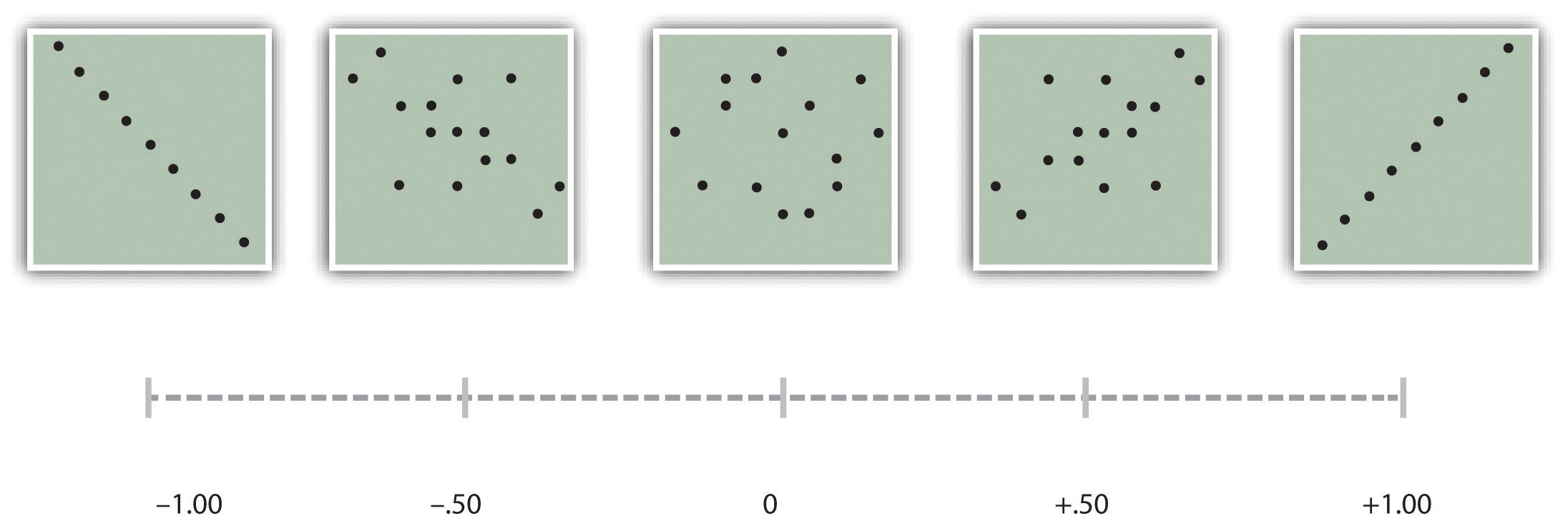
Как мы видели ранее в книге, сила корреляции между количественными переменными обычно измеряется с помощью статистики, называемой r Пирсона . Как показано на рис. 12.10, «коэффициент Пирсона» может принимать значения от -1,00 до нуля и +1,00. Значение 0 означает, что между двумя переменными нет связи. В дополнение к своим рекомендациям по интерпретации d Коэна, Коэн предложил рекомендации по интерпретации r Пирсона в психологических исследованиях (см. Таблицу 12.4 «Рекомендации по использованию Коэна» ). Значения около ± 0,10 считаются малыми, значения около ± 0,30 считаются средними, а значения около ± 0,50 считаются большими. Обратите внимание, что знак Пирсона rне зависит от его силы. Например, значения r Пирсона +, 30 и -0,30 одинаково сильны; просто одно представляет умеренное положительное отношение, а другое умеренное отрицательное отношение. Подобно d Коэна , r Пирсона также называют мерой «величины эффекта», хотя связь может и не быть причинно-следственной.

Рис. 12.10 Диапазон значений r Пирсона от –1,00 (представляет самую сильную возможную отрицательную связь), через 0 (представляющую отсутствие связи) до +1,00 (представляющую самую сильную возможную положительную связь)

Вычисления для r Пирсона более сложны, чем для d Коэна . Хотя вам, возможно, никогда не придется делать их вручную, все же поучительно посмотреть, как это сделать. В вычислительном отношении r Пирсона представляет собой «среднее перекрестное произведение z - баллов». Чтобы вычислить его, нужно начать с преобразования всех оценок в z - оценки. Для переменной X вычтите среднее значение X из каждой оценки и разделите каждую разницу на стандартное отклонение X . Для переменной Y вычтите среднее значение Y из каждой оценки и разделите каждую разницу на стандартное отклонение Y.. Затем для каждого человека умножьте два показателя z вместе, чтобы получить перекрестный продукт. Наконец, возьмите среднее значение перекрестных произведений. Формула выглядит следующим образом:

$$$$

Таблица 12.5 «Примеры вычислений для Пирсона» иллюстрируют эти вычисления для небольшого набора данных. В первом столбце перечислены баллы для переменной X , которая имеет среднее значение 4,00 и стандартное отклонение 1,90. Второй столбец представляет собой оценку z для каждой из этих необработанных оценок. В третьем и четвертом столбцах перечислены необработанные оценки для переменной Y , которая имеет среднее значение 40 и стандартное отклонение 11,78, а также соответствующие оценки z . В пятой колонке перечислены перекрестные продукты. Например, первый равен 0,00, умноженному на -0,85, что равно 0,00. Второй равен 1,58, умноженному на 1,19, что равно 1,88. Среднее значение этих перекрестных произведений, показанное внизу этой колонки, равно r Пирсона., что в данном случае равно +0,53. Существуют и другие формулы для вычисления r Пирсона вручную, которые могут быть быстрее. Этот подход, однако, гораздо яснее с точки зрения концептуальной передачи того, что такое пирсоновское r .

Таблица 12.5 Примеры вычислений для Пирсона r

Икс	г х	Д	г у	г х г у
4	0,00	30	−0,85	0,00
7	1,58	54	1.19	1,88
2	−1,05	23	−1,44	1,52
5	0,53	43	0,26	0,13
2	−1,05	50	0,85	−0,89
М х = 4,00		М г = 40,00		г = 0,53
SD х = 1,90		SD у = 11,78

Есть две распространенные ситуации, в которых значение r Пирсона может ввести в заблуждение. Во-первых, когда изучаемые отношения нелинейны. Хотя на рис. 12.9 «Гипотетическая нелинейная зависимость между тем, сколько человек спит за ночь, и тем, насколько они подавлены» показана довольно сильная связь между депрессией и сном, r Пирсона будет близок к нулю, поскольку точки на диаграмме рассеяния не совсем совпадают. одной прямой линией. Это означает, что важно построить диаграмму рассеяния и убедиться, что связь приблизительно линейна, прежде чем использовать r Пирсона . Другой — когда одна или обе переменные имеют ограниченный диапазон в выборке по сравнению с генеральной совокупностью. Это называетсяограничение ассортимента . Предположим, например, что существует сильная отрицательная корреляция между возрастом людей и их увлечением хип-хопом, как показано на диаграмме рассеяния на рис. Диапазон» . Здесь r Пирсонасоставляет −0,77. Однако, если бы мы собирали данные только о подростках в возрасте от 18 до 24 лет, представленные заштрихованной областью на рис. 12.11 «Гипотетические данные, показывающие, как сильная общая корреляция может казаться слабой, когда одна переменная имеет ограниченный диапазон» — тогда связь будет казаться довольно слабой. На самом деле, г Пирсонадля этого ограниченного диапазона возрастов равен 0. Поэтому было бы неплохо спланировать исследования так, чтобы избежать ограничения диапазона. Например, если возраст является одной из ваших основных переменных, вы можете запланировать сбор данных от людей самых разных возрастов. Однако, поскольку ограничение диапазона не всегда можно предвидеть или легко избежать, хорошей практикой является проверка ваших данных на предмет возможного ограничения диапазона и интерпретация r Пирсона в свете этого. (Существуют также статистические методы коррекции пирсоновского r для ограничения диапазона, но они выходят за рамки этой книги).

Рис. 12.11 . Гипотетические данные, показывающие, как сильная общая корреляция может оказаться слабой, когда одна переменная имеет ограниченный диапазон

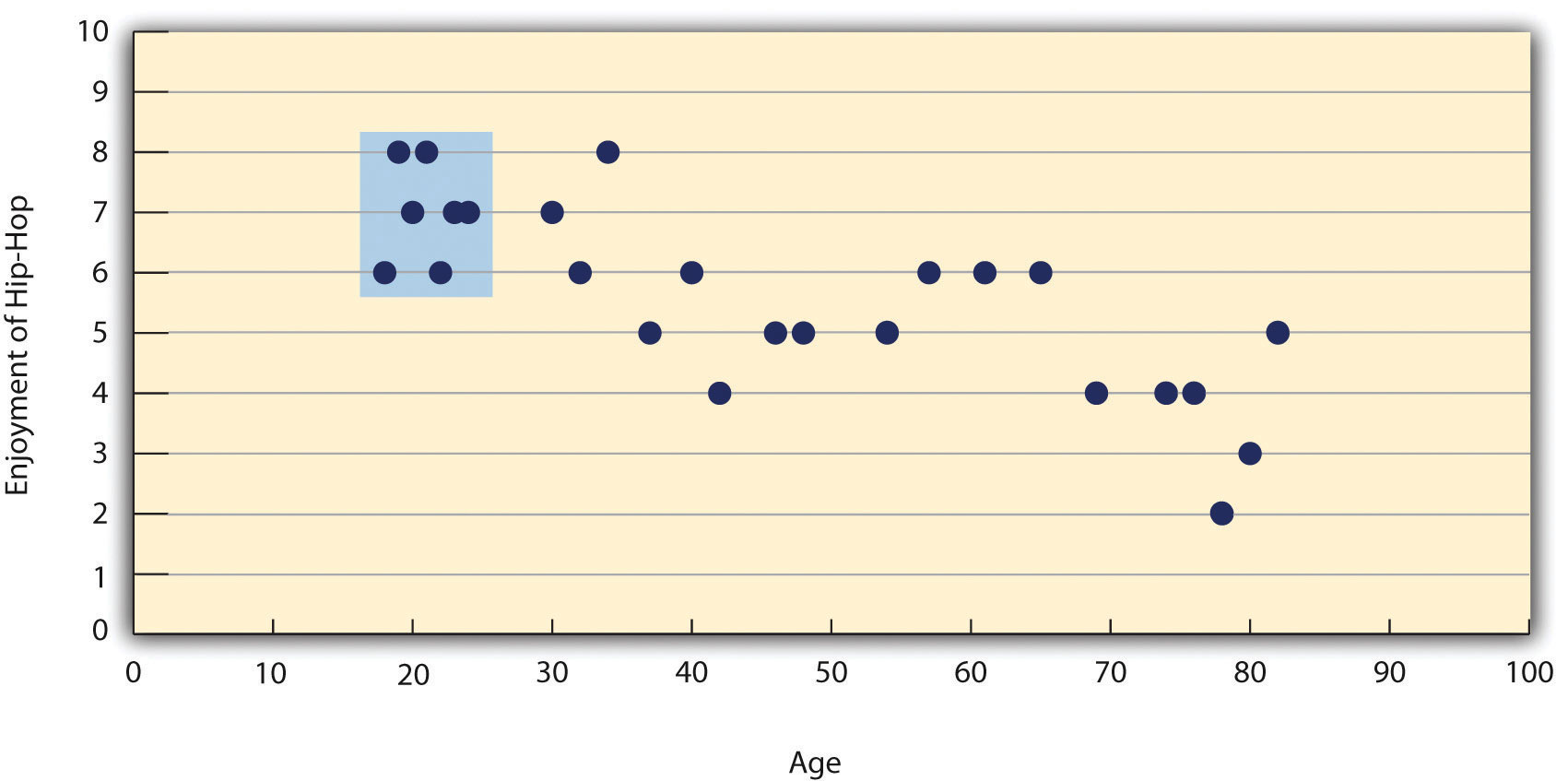
Общая корреляция здесь составляет -0,77, но корреляция для 18-24-летних (в синей рамке) равна 0.

КЛЮЧЕВЫЕ ВЫВОДЫ

• Различия между группами или состояниями обычно описываются в терминах средних значений и стандартных отклонений групп или условий или в терминах d Коэна и представляются в виде гистограмм.
• Коэнов d является мерой силы связи (или размера эффекта) для различий между двумя средними группами или состояниями. Это разница средних, деленная на стандартное отклонение. Как правило, значения ±0,20, ±0,50 и ±0,80 можно считать малыми, средними и большими соответственно.
• Корреляции между количественными переменными обычно описываются в терминах r Пирсона и представляются в виде линейных графиков или диаграмм рассеяния.
• Коэффициент Пирсона является мерой силы взаимосвязи (или размера эффекта) для взаимосвязей между количественными переменными. Это среднее перекрестное произведение двух наборов z - показателей. Как правило, значения ±0,10, ±0,30 и ±0,50 можно считать малыми, средними и большими соответственно.

УПРАЖНЕНИЯ

1. Практика: Следующие данные представляют собой баллы по шкале самооценки Розенберга для выборки из 10 японских студентов колледжей и 10 американских студентов колледжей. (Хотя эти данные и являются гипотетическими, они согласуются с эмпирическими данными [Schmitt & Allik, 2005]. Schmitt, DP, & Allik, J. (2005). Одновременное применение шкалы самооценки Розенберга в 53 странах: изучение универсального и культурного специфические особенности общей самооценки Journal of Personality and Social Psychology, 89 , 623–642. ) Вычислите средние значения и стандартные отклонения для двух групп, постройте столбчатую диаграмму, вычислите коэффициент Коэна d и опишите силу взаимосвязи. в словах.

   Япония	Соединенные Штаты
   25	27
   20	30
   24	34
   28	37
   30	26
   32	24
   21	28
   24	35
   20	33
   26	36

2. Практика. Нижеследующие гипотетические данные — это показатели экстраверсии и количество друзей на Facebook для 15 студентов колледжа. Постройте диаграмму рассеяния для этих данных, вычислите r Пирсона и опишите взаимосвязь словами.

   Экстраверсия	друзья на фейсбуке
   8	75
   10	315
   4	28
   6	214
   12	176
   14	95
   10	120
   11	150
   4	32
   13	250
   5	99
   7	136
   8	185
   11	88
   10	144

12.3 Выражение результатов

ЦЕЛИ ОБУЧЕНИЯ

1. Напишите простую описательную статистику в стиле Американской психологической ассоциации (АПА).
2. Интерпретируйте и создавайте простые графики в стиле APA, включая гистограммы, линейные графики и диаграммы рассеяния.
3. Интерпретируйте и создавайте простые таблицы в стиле APA, включая таблицы средних значений групп или условий и корреляционные матрицы.

После того, как вы провели свой описательный статистический анализ, вам нужно будет представить его другим. В этом разделе мы сосредоточимся на представлении описательных статистических результатов в письменной форме, на графиках и в таблицах, следуя рекомендациям Американской психологической ассоциации (АПА) для письменных отчетов об исследованиях. Эти принципы можно легко адаптировать к другим форматам презентаций, таким как плакаты и слайд-шоу.

Представление описательной статистики в письменной форме

Когда у вас есть небольшое количество результатов для отчета, зачастую наиболее эффективно записывать их. Здесь есть несколько важных рекомендаций по стилю APA. Во-первых, статистические результаты всегда представляются в виде цифр, а не слов, и обычно округляются до двух знаков после запятой (например, «2,00», а не «два» или «2»). Они могут быть представлены либо в описательном описании результатов, либо в скобках, подобно ссылкам на источники. Вот некоторые примеры:

Средний возраст участников составил 22,43 года со стандартным отклонением 2,34.

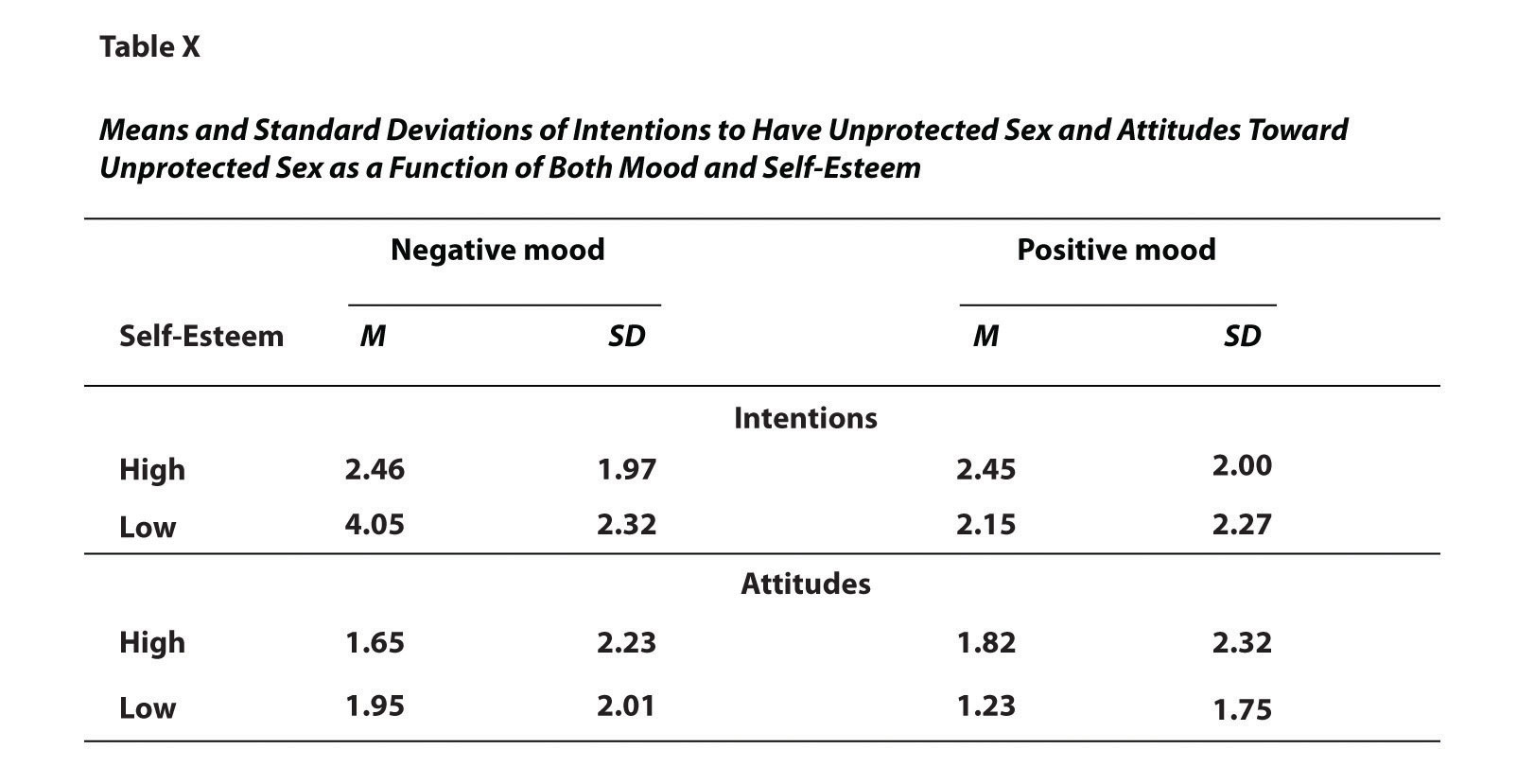
Среди участников с низкой самооценкой те, кто находился в негативном настроении, выражали более сильное намерение заниматься незащищенным сексом ( M = 4,05, SD = 2,32), чем те, кто находился в позитивном настроении ( M = 2,15, SD = 2,27).

В группе лечения среднее значение составило 23,40 ( SD = 9,33), в то время как в контрольной группе среднее значение составило 20,87 ( SD = 8,45).

Корреляция между тестом и повторным тестом составила 0,96.

Между положением фамилий респондентов в алфавитном порядке и временем их ответа наблюдалась умеренная отрицательная корреляция ( r = -0,27).

Обратите внимание, что при представлении в описательной части термины « среднее » и « стандартное отклонение » выписаны, но при представлении в скобках вместо них используются символы M и SD . Обратите также внимание на то, что использование параллельного построения особенно важно для выражения сходных или сравнимых результатов сходными способами. Третий пример намного лучше, чем следующая непараллельная альтернатива:

Группа лечения имела среднее значение 23,40 ( SD = 9,33), в то время как 20,87 было средним значением контрольной группы, у которой было стандартное отклонение 8,45.

Представление описательной статистики в виде графиков

Когда у вас есть большое количество результатов для отчета, вы часто можете сделать это более четко и эффективно с помощью графика. Когда вы готовите графики для исследовательского отчета в стиле APA, вам следует помнить о некоторых общих рекомендациях. Во-первых, график всегда должен добавлять важную информацию, а не повторять информацию, которая уже присутствует в тексте или в таблице. (Если диаграмма представляет информацию более четко или эффективно, вам следует сохранить диаграмму и исключить текст или таблицу.) Во-вторых, диаграммы должны быть как можно более простыми. Например, Руководство по публикациине поощряет использование цвета, если в этом нет абсолютной необходимости (хотя цвет по-прежнему может быть эффективным элементом плакатов, презентаций в виде слайд-шоу или учебников). В-третьих, графики должны интерпретироваться сами по себе. Читатель должен быть в состоянии понять основной результат, основываясь только на графике и его подписи, и ему не нужно обращаться к тексту для объяснения.

Существует также еще несколько технических рекомендаций для графиков, которые включают следующее:

• Макет

  • График должен быть немного шире, чем высота.
  • Независимая переменная должна быть нанесена на ось абсцисс , а зависимая переменная — на ось у .
  • Значения должны увеличиваться слева направо по оси x и снизу вверх по оси y .

• Ярлыки и легенды оси

  • Метки осей должны быть четкими и лаконичными и включать единицы измерения, если они не указаны в подписи.
  • Метки осей должны быть параллельны оси.
  • Легенды должны появляться в границах графика.
  • Текст должен быть набран одним и тем же простым шрифтом и отличаться не более чем на четыре пункта.

• Подписи

  • Подписи должны кратко описывать рисунок, объяснять любые сокращения и включать единицы измерения, если они не отображаются в метках осей.
  • Подписи в рукописи APA должны быть напечатаны на отдельной странице в конце рукописи. Дополнительную информацию см. в главе 11 «Представление вашего исследования» .

Гистограммы

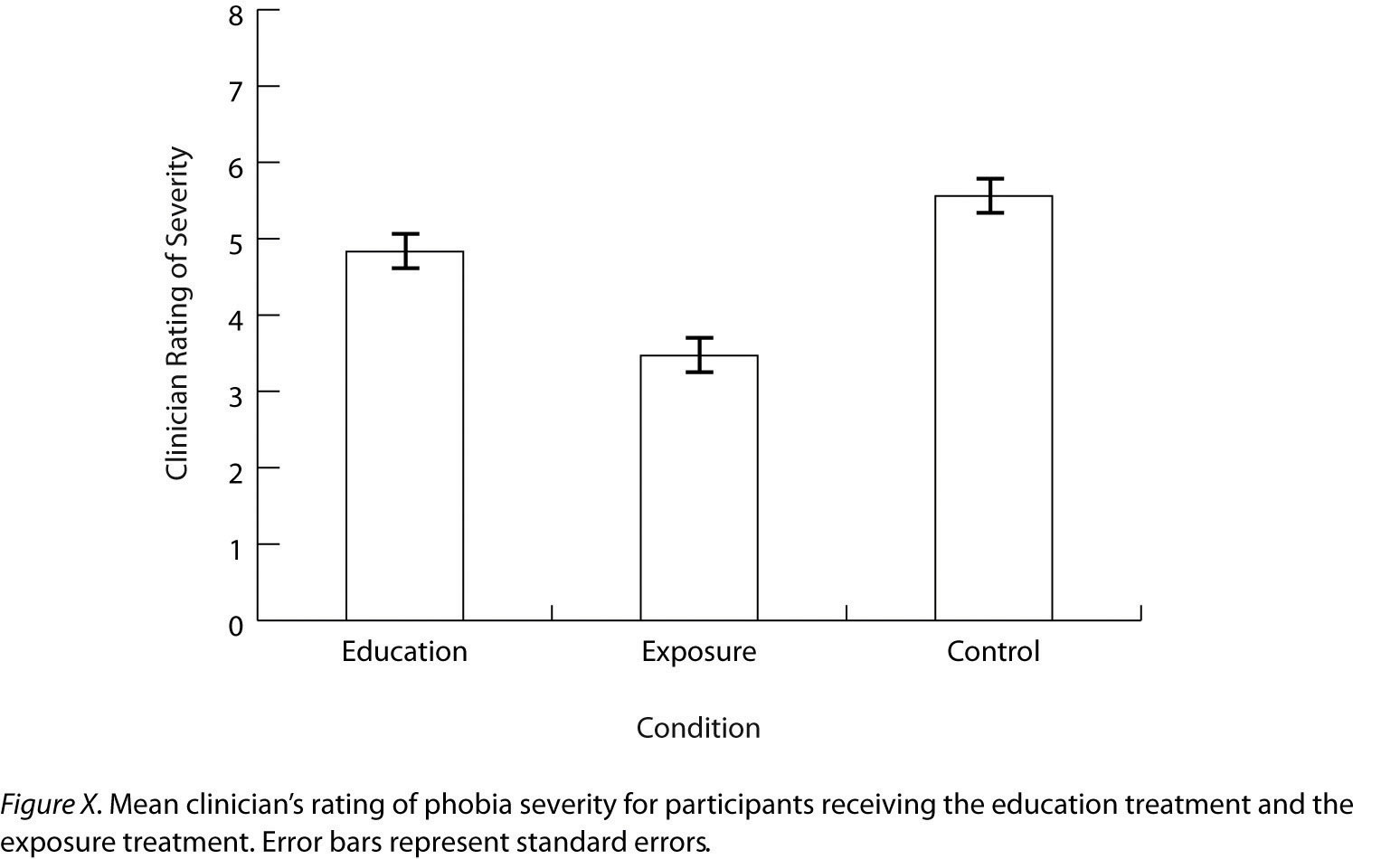
Как мы видели в этой книге, гистограммы обычно используются для представления и сравнения средних показателей для двух или более групп или состояний. Гистограмма на рис. 12.12 «Образец гистограммы в стиле APA с планками погрешностей, представляющими стандартные ошибки, основанный на исследовании Оллендика и его коллег» представляет собой версию в стиле APA рис. Два состояния лечения» . Обратите внимание, что он соответствует всем перечисленным рекомендациям. Новый элемент на рис. 12.12 «Образец гистограммы в стиле APA с планками погрешностей, представляющими стандартные ошибки, на основе исследования Оллендика и его коллег».это меньшие вертикальные полосы, которые простираются как вверх, так и вниз от вершины каждой основной полосы. Это планки погрешностей , и они представляют изменчивость в каждой группе или состоянии. Хотя они иногда расширяют одно стандартное отклонение в каждом направлении, они с большей вероятностью увеличивают одну стандартную ошибку в каждом направлении (как на рис. Коллеги» ). Стандартная ошибкапредставляет собой стандартное отклонение группы, деленное на квадратный корень из размера выборки группы. Стандартная ошибка используется потому, что, как правило, разница между средними группами, превышающая две стандартные ошибки, является статистически значимой. Таким образом, можно «увидеть», является ли различие статистически значимым, на основе гистограммы с планками погрешностей.

Рисунок 12.12 . Пример гистограммы в стиле APA с планками погрешностей, представляющими стандартные ошибки, на основе исследования Оллендика и его коллег.

Линейные графики

Линейные графики используются для представления корреляций между количественными переменными, когда независимая переменная имеет или организована в относительно небольшое количество различных уровней. Каждая точка на линейном графике представляет собой средний балл по зависимой переменной для участников на одном уровне независимой переменной. Рисунок 12.13 «Пример линейного графика в стиле APA, основанный на исследованиях Карлсона и Конарда» представляет собой версию результатов Карлсона и Конарда в стиле APA. Обратите внимание, что он включает планки погрешностей, представляющие стандартную ошибку, и соответствует всем заявленным рекомендациям.

Рис. 12.13 . Пример линейного графика в стиле APA, основанный на исследованиях Карлсона и Конарда.

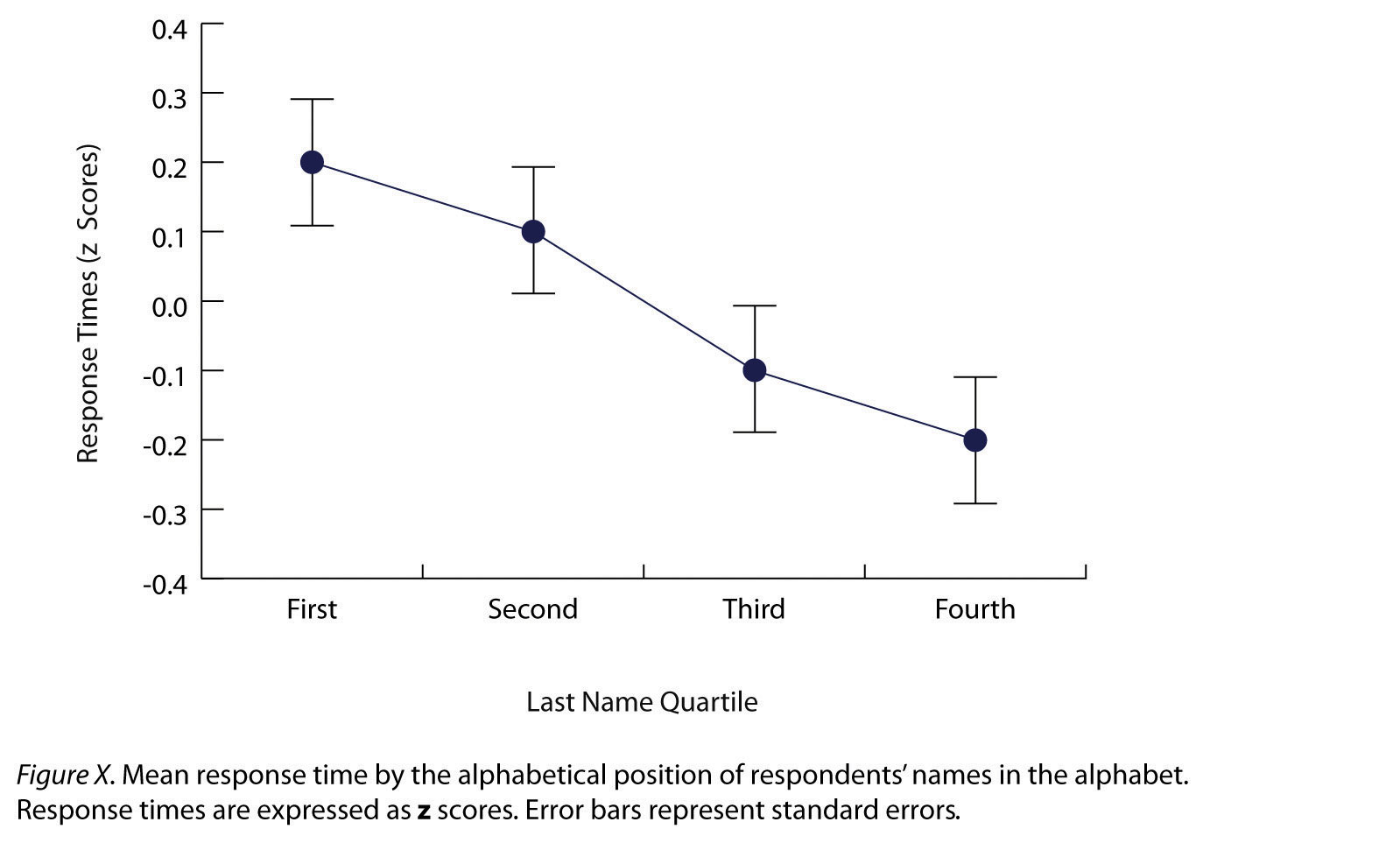
In most cases, the information in a line graph could just as easily be presented in a bar graph. In Figure 12.13 "Sample APA-Style Line Graph Based on Research by Carlson and Conard", for example, one could replace each point with a bar that reaches up to the same level and leave the error bars right where they are. This emphasizes the fundamental similarity of the two types of statistical relationship. Both are differences in the average score on one variable across levels of another. The convention followed by most researchers, however, is to use a bar graph when the variable plotted on the x-axis is categorical and a line graph when it is quantitative.

Scatterplots

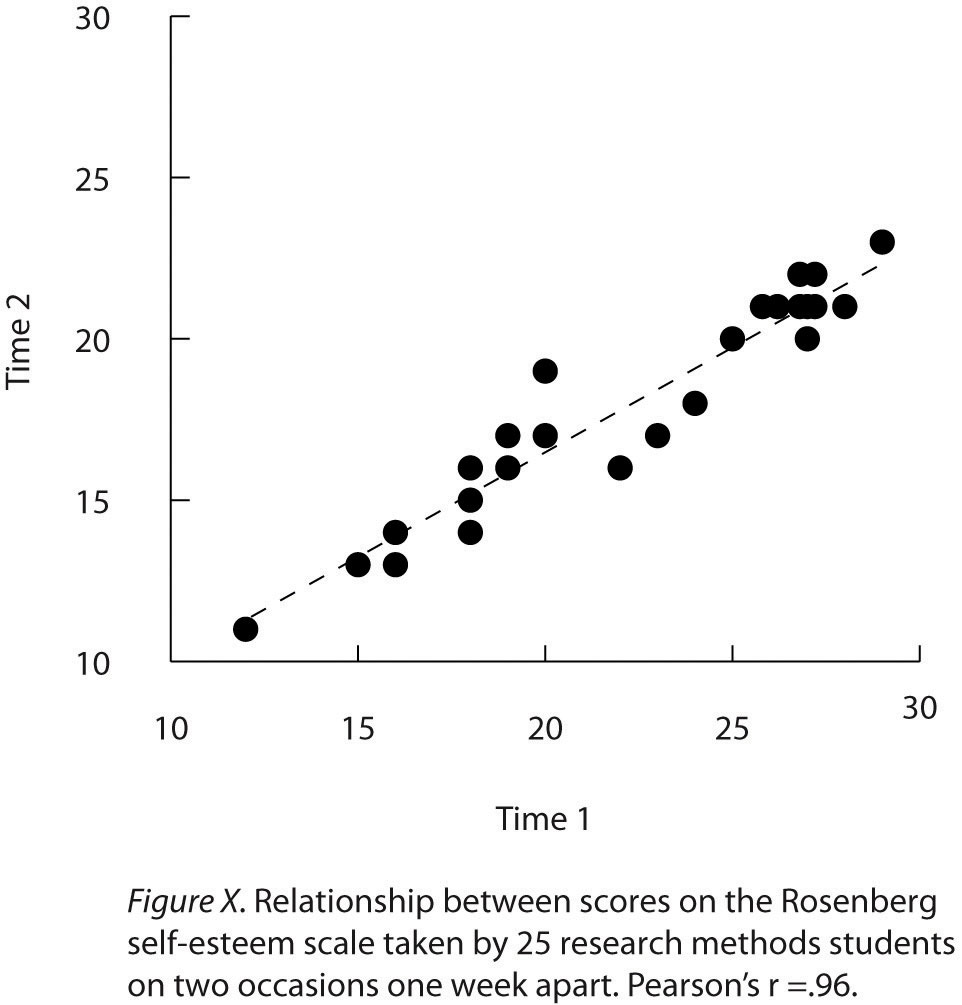
Диаграммы рассеяния используются для представления отношений между количественными переменными, когда переменная на оси x (обычно независимая переменная) имеет большое количество уровней. Каждая точка на диаграмме рассеяния представляет человека, а не среднее значение для группы людей, и нет линий, соединяющих точки. График на рисунке 12.14 «Образец диаграммы рассеяния в стиле APA» представляет собой версию в стиле APA рисунка 12.8 «Статистическая взаимосвязь между оценками нескольких студентов колледжа по шкале самооценки Розенберга, полученной два раза с разницей в неделю» , которая иллюстрирует несколько дополнительные баллы. Во-первых, когда переменные пооси x и y-оси концептуально похожи и измеряются в одной шкале - как здесь, где они являются мерами одной и той же переменной в двух разных случаях - это можно подчеркнуть, сделав оси одинаковой длины. Во-вторых, когда два или более человека попадают в одну и ту же точку на графике, один из способов указать на это — слегка сместить точки по оси X. Другие способы заключаются в отображении количества особей в скобках рядом с точкой или в увеличении или уменьшении размера точки пропорционально количеству особей. Наконец, также может быть включена прямая линия, которая лучше всего соответствует точкам на диаграмме рассеяния, называемая линией регрессии.

Рисунок 12.14 Пример диаграммы рассеяния в стиле APA

Выражение описательной статистики в таблицах

Как и графики, таблицы можно использовать для четкого и эффективного представления больших объемов информации. К таблицам применяются те же общие принципы, что и к графикам. Они должны добавлять важную информацию к представлению ваших результатов, быть как можно более простыми и интерпретируемыми сами по себе. Опять же, мы сосредоточимся здесь на таблицах для рукописи в стиле APA.

Чаще всего таблицы используются для представления нескольких средних значений и стандартных отклонений — обычно для сложных планов исследований с множеством независимых и зависимых переменных. На рисунке 12.15 «Образец таблицы в стиле APA, представляющей средние значения и стандартные отклонения» , например, показаны результаты гипотетического исследования, аналогичного исследованию, проведенному MacDonald and Martineau (2002) MacDonald, TK, & Martineau, AM (2002). Самооценка, настроение и намерения использовать презервативы: когда низкая самооценка приводит к опасному для здоровья поведению? Журнал экспериментальной социальной психологии, 38 , 299–306. обсуждалось в главе 5 «Психологические измерения» . (Средние значения на рисунке 12.15 «Образец таблицы в стиле APA, представляющей средние значения и стандартные отклонения»являются средними значениями, указанными Макдональдом и Мартино, но не стандартными ошибками). Напомним, что эти исследователи классифицировали участников с низкой или высокой самооценкой, помещали их в негативное или позитивное настроение и измеряли их намерения заниматься незащищенным сексом. Хотя это и не упоминается в главе 5 «Психологические измерения»., они также измерили отношение участников к незащищенному сексу. Обратите внимание, что таблица включает горизонтальные линии, охватывающие всю таблицу вверху и внизу, а также непосредственно под заголовками столбцов. Кроме того, у каждого столбца есть заголовок, включая крайний левый столбец, а также дополнительные заголовки, охватывающие два или более столбца, которые помогают организовать информацию и представить ее более эффективно. Наконец, обратите внимание, что таблицы в стиле APA нумеруются последовательно, начиная с 1 (таблица 1, таблица 2 и т. д.), и имеют краткие, но ясные и описательные заголовки.

Рисунок 12.15 Пример таблицы в стиле APA, в которой представлены средние значения и стандартные отклонения

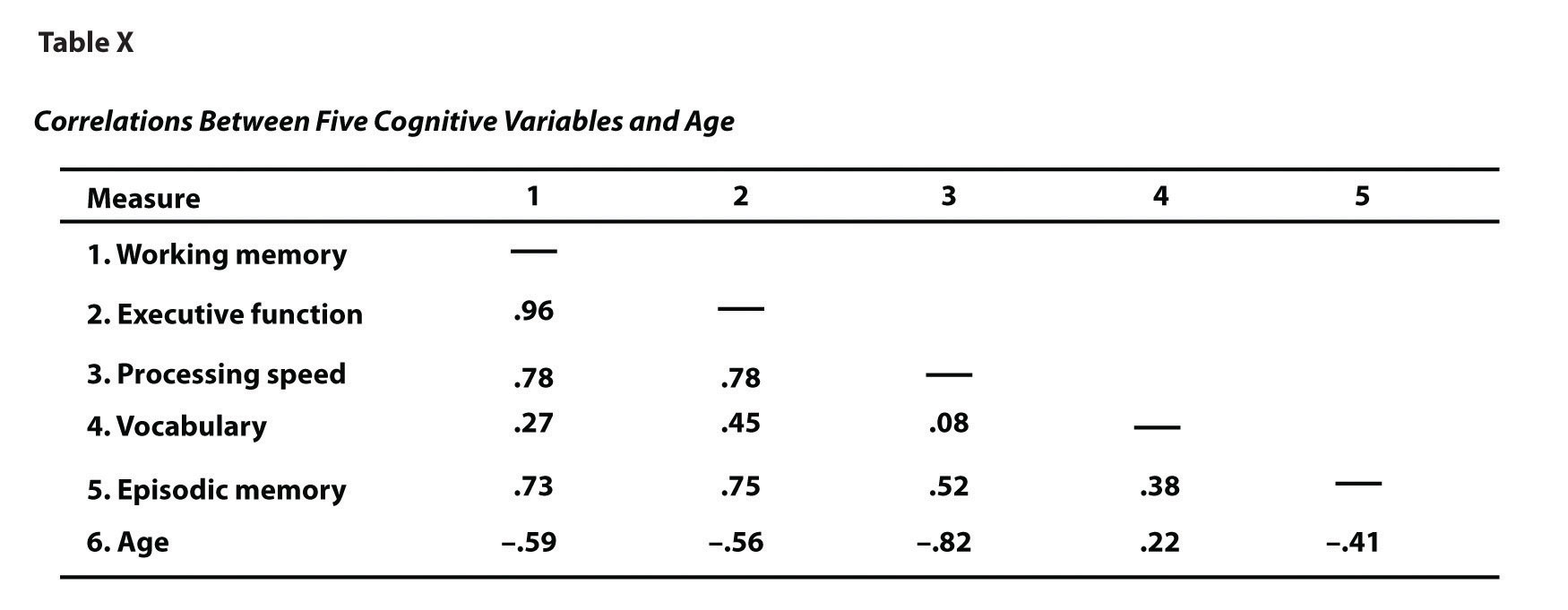
Еще одно распространенное использование таблиц — представление корреляций — обычно измеряемых с помощью r Пирсона — между несколькими переменными. Это называется корреляционной матрицей . Рисунок 12.16 «Пример таблицы в стиле APA (матрица корреляции) на основе исследования Маккейба и его коллег» — это матрица корреляции, основанная на исследовании Дэвида Маккейба и его коллег (McCabe, Roediger, McDaniel, Balota, & Hambrick, 2010). Маккейб, Д.П., Редигер, Х.Л., Макдэниел, М.А., Балота, Д.А., и Хамбрик, Д.З. (2010). Взаимосвязь между объемом рабочей памяти и исполнительным функционированием. Нейропсихология, 243 , 222–243.Их интересовали отношения между рабочей памятью и некоторыми другими переменными. Из таблицы видно, что корреляция между рабочей памятью и исполнительной функцией, например, была чрезвычайно сильной 0,96, что корреляция между рабочей памятью и словарным запасом была средней 0,27 и что все показатели, кроме словарного запаса, имеют тенденцию к снижению. с возрастом. Обратите внимание, что заполнена только половина таблицы, потому что другая половина будет иметь идентичные значения. Например, значение r Пирсона в правом верхнем углу (рабочая память и возраст) будет таким же, как и в левом нижнем углу (возраст и рабочая память). Корреляция переменной сама с собой всегда равна 1,00, поэтому эти значения заменены тире, чтобы облегчить чтение таблицы.

Рисунок 12.16 Пример таблицы в стиле APA (матрица корреляции), основанный на исследовании Маккейба и его коллег

Как и в случае с графиками, точные статистические результаты, приведенные в таблице, необязательно повторять в тексте. Вместо этого автор может отметить основные тенденции и предупредить читателя о деталях (например, конкретных корреляциях), которые представляют особый интерес.

КЛЮЧЕВЫЕ ВЫВОДЫ

• В статье в стиле APA простые результаты наиболее эффективно представлены в тексте, тогда как более сложные результаты наиболее эффективно представлены в виде графиков или таблиц.
• Стиль АРА включает в себя несколько правил представления числовых результатов в тексте. К ним относятся использование слов только для чисел меньше 10, которые не представляют точных статистических результатов, и округление результатов до двух знаков после запятой с использованием слов (например, «среднее») в тексте и символов (например, « М ») в круглых скобках.
• Стиль APA включает в себя несколько правил представления результатов в виде графиков и таблиц. Графики и таблицы должны добавлять информацию, а не повторяться, быть как можно более простыми и интерпретируемыми сами по себе с описательным заголовком (для графиков) или описательным заголовком (для таблиц).

УПРАЖНЕНИЕ

1. Практика. В классическом исследовании мужчины и женщины оценивали важность физической привлекательности как для краткосрочного, так и для долгосрочного партнера (Buss & Schmitt, 1993). Басс, Д.М., и Шмитт, Д.П. (1993). Теория сексуальных стратегий: контекстуальный эволюционный анализ человеческого спаривания. Психологический обзор, 100 , 204–232. Средние значения и стандартные отклонения следующие. Мужчины / Краткосрочные: M = 5,67, SD = 2,34; Мужчины/долгосрочные: M = 4,43, SD = 2,11; Женщины / краткосрочные: M = 5,67, SD = 2,48; Женщины / Долгий срок: M = 4,22, SD= 1,98. Представьте эти результаты (а) в письменной форме, (б) в виде графика и (в) в таблице.

12.4 Проведение анализов

ЗАДАЧА ОБУЧЕНИЯ

1. Опишите шаги, связанные с подготовкой и анализом типичного набора необработанных данных.

Даже когда вы понимаете, что касается статистики, анализ данных может быть сложным процессом. Вполне вероятно, что для каждого из нескольких участников имеются данные по нескольким различным переменным: демографические данные, такие как пол и возраст, одна или несколько независимых переменных, одна или несколько зависимых переменных и, возможно, проверка манипулирования. Более того, «сырые» (непроанализированные) данные могут принимать несколько различных форм — заполненные бумажно-карандашные вопросники, компьютерные файлы, заполненные цифрами или текстом, видео или письменные заметки, — и их, возможно, придется систематизировать, кодировать или комбинировать. каким-то образом. Могут быть даже отсутствующие, неправильные или просто «подозрительные» ответы, с которыми необходимо разобраться. В этом разделе мы рассмотрим некоторые практические советы, чтобы сделать этот процесс максимально организованным и эффективным.

Подготовьте данные для анализа

Независимо от того, находятся ли ваши необработанные данные на бумаге или в компьютерном файле (или в том и другом), есть несколько вещей, которые вы должны сделать, прежде чем приступить к их анализу. Во-первых, убедитесь, что они не содержат никакой информации, которая может идентифицировать отдельных участников, и убедитесь, что у вас есть безопасное место, где вы можете хранить данные, и отдельное безопасное место, где вы можете хранить любые формы согласия. Если данные не являются очень конфиденциальными, обычно достаточно запертой комнаты или защищенного паролем компьютера. Также рекомендуется делать фотокопии или резервные копии файлов ваших данных и хранить их в еще одном безопасном месте — по крайней мере, до завершения проекта. Профессиональные исследователи обычно хранят копии своих необработанных данных и форм согласия в течение нескольких лет на случай, если после завершения проекта возникнут вопросы о процедуре, данных или согласии участников.

Затем вы должны проверить свои необработанные данныечтобы убедиться, что они заполнены и выглядят точно записанными (будь то участники, вы сами или компьютерная программа, которая делала запись). На этом этапе вы можете обнаружить неразборчивые или отсутствующие ответы или явное недопонимание (например, ответ «12» по шкале от 1 до 10). Вам придется решить, достаточно ли серьезны такие проблемы, чтобы сделать данные участника непригодными для использования. Если информация об основной независимой или зависимой переменной отсутствует, или если несколько ответов отсутствуют или вызывают подозрения, возможно, вам придется исключить данные этого участника из анализа. Если вы решите исключить какие-либо данные, не выбрасывайте и не удаляйте их, потому что вы или другой исследователь можете захотеть просмотреть их позже. Вместо,

Теперь вы готовы ввести свои данные в программу для работы с электронными таблицами или, если они уже есть в компьютерном файле, отформатировать их для анализа. Для создания файла данных можно использовать обычную программу для работы с электронными таблицами, например Microsoft Excel, или программу статистического анализа, например SPSS . (Файлы данных, созданные в одной программе, обычно можно преобразовать для работы с другими программами.) Наиболее распространенный формат: каждая строка представляет участника, а каждый столбец представляет переменную (с именем переменной вверху каждого столбца). . Пример файла данных показан в таблице 12.6 «Пример файла данных».. Первый столбец содержит идентификационные номера участников. Затем следуют столбцы, содержащие демографическую информацию (пол и возраст), независимые переменные (настроение, четыре элемента самооценки и общее количество четырех элементов самооценки) и, наконец, зависимые переменные (намерения и установки). Категориальные переменные обычно можно вводить в виде меток категорий (например, «М» и «Ж» для мужчин и женщин) или в виде чисел (например, «0» для отрицательного настроения и «1» для положительного настроения). Хотя метки категорий часто более четкие, для некоторых анализов могут потребоваться числа. SPSS позволяет вам вводить числа, а также прикреплять к каждому числу метку категории.

Таблица 12.6 Пример файла данных

Я БЫ	СЕКС	ВОЗРАСТ	НАСТРОЕНИЕ	SE1	SE2	SE3	SE4	ОБЩИЙ	INT	АТТ
1	М	20	1	2	3	2	3	10	6	5
2	Ф	22	1	1	0	2	1	4	4	4
3	Ф	19	0	2	2	2	2	8	2	3
4	Ф	24	0	3	3	2	3	11	5	6

Если у вас есть критерии множественного ответа — например, показатель самооценки в Таблице 12.6 «Пример файла данных» , — вы можете комбинировать элементы вручную, а затем ввести общий балл в свою электронную таблицу. Однако намного лучше вводить каждый ответ как отдельную переменную в электронную таблицу — как в случае показателя самооценки в Таблице 12.6 «Файл с примерными данными» — и использовать программное обеспечение для их объединения (например, с помощью функции «СРЕДНЯЯ»). в Excel или функцию «Вычислить» в SPSS). Этот подход не только более точен, но и позволяет обнаруживать и исправлять ошибки, оценивать внутреннюю согласованность и анализировать отдельные ответы, если вы решите сделать это позже.

Предварительные анализы

Прежде чем перейти к основным вопросам исследования, часто необходимо провести несколько предварительных анализов. Для мер с множественными ответами следует оценить внутреннюю согласованность меры. Статистические программы, такие как SPSS, позволят вам вычислить α Кронбаха или κ Коэна. Если это выходит за рамки вашего уровня комфорта, вы все равно можете вычислить и оценить корреляцию с разделением пополам.

Далее следует проанализировать каждую важную переменную отдельно. (Конечно, это не обязательно для управляемых независимых переменных, потому что вы, как исследователь, определили, каким будет распределение.) Составьте гистограммы для каждой из них, отметьте их форму и вычислите общие показатели центральной тенденции и изменчивости. Убедитесь, что вы понимаете, что означают эти статистические данные с точки зрения интересующих вас переменных. Например, распределение самооценки счастья по шкале от 1 до 10 может быть унимодальным и иметь отрицательную асимметрию со средним значением 8,25. и стандартное отклонение 1,14. Но это означает , что большинство участников оценили себя довольно высоко по шкале счастья, а небольшое число оценило себя заметно ниже.

Настало время выявить выбросы, изучить их более внимательно и решить, что с ними делать. Вы можете обнаружить, что то, что на первый взгляд кажется выбросом, является результатом неправильного ввода ответа в файл данных, и в этом случае вам нужно только исправить файл данных и двигаться дальше. В качестве альтернативы вы можете подозревать, что выброс представляет собой какую-то другую ошибку, непонимание или отсутствие усилий со стороны участника. Например, в распределении времени реакции, в котором большинству участников потребовалось всего несколько секунд, чтобы ответить, участник, которому потребовалось 3 минуты, чтобы ответить, будет выбросом. Кажется вероятным, что этот участник не понял задание (или, по крайней мере, не обратил на него особого внимания). Кроме того, включение его или ее времени реакции окажет большое влияние на среднее значение и стандартное отклонение для выборки. В подобных ситуациях может быть оправданным исключение из анализа второстепенного ответа или участника. Однако если вы сделаете это, вам следует вести записи о том, какие ответы или участников вы исключили и почему, и последовательно применять те же критерии к каждому ответу и каждому участнику. Когда вы представляете свои результаты, вы должны указать, сколько ответов или участников вы исключили, а также конкретные критерии, которые вы использовали. И опять же, не выбрасывайте и не удаляйте данные, которые вы решили исключить. Просто отложите их, потому что вы или другой исследователь можете захотеть просмотреть их позже. и последовательно применяйте те же самые критерии к каждому ответу и каждому участнику. Когда вы представляете свои результаты, вы должны указать, сколько ответов или участников вы исключили, а также конкретные критерии, которые вы использовали. И опять же, не выбрасывайте и не удаляйте данные, которые вы решили исключить. Просто отложите их, потому что вы или другой исследователь можете захотеть просмотреть их позже. и последовательно применяйте те же самые критерии к каждому ответу и каждому участнику. Когда вы представляете свои результаты, вы должны указать, сколько ответов или участников вы исключили, а также конкретные критерии, которые вы использовали. И опять же, не выбрасывайте и не удаляйте данные, которые вы решили исключить. Просто отложите их, потому что вы или другой исследователь можете захотеть просмотреть их позже.

Имейте в виду, что выбросы не обязательно означают ошибку, непонимание или недостаток усилий. Они могут представлять действительно экстремальные ответы или участников. Например, в одной большой выборке студентов колледжа подавляющее большинство участников сообщили, что у них было менее 15 сексуальных партнеров, но также было несколько крайних значений 60 или 70 (Brown & Sinclair, 1999). Браун, Н.Р., и Синклер, Р.К. (1999). Оценка количества сексуальных партнеров в течение жизни: мужчины и женщины делают это по-разному. Журнал сексуальных исследований, 36 , 292–297.Хотя эти оценки могут отражать ошибки, недоразумения или даже преднамеренные преувеличения, вполне вероятно, что они представляют собой честные и даже точные оценки. Одной из стратегий здесь было бы использование медианы и других статистических данных, на которые не сильно влияют выбросы. Другой вариант — проанализировать данные, включая и исключая любые выбросы. Если результаты в основном совпадают, что часто бывает, то имеет смысл оставить выбросы. Если результаты различаются в зависимости от того, включены или исключены выбросы, то можно представить оба анализа и обсудить различия между ними.

Ответьте на вопросы исследования

Наконец, вы готовы ответить на основные вопросы исследования. Если вас интересует разница между средними значениями группы или условия, вы можете вычислить соответствующие средние значения группы или условия и стандартные отклонения, построить гистограмму для отображения результатов и вычислить d Коэна . Если вас интересует корреляция между количественными переменными, вы можете построить линейный график или диаграмму рассеяния (не забудьте проверить на нелинейность и ограничение диапазона) и вычислить r Пирсона .

На этом этапе вы также должны изучить свои данные на предмет других интересных результатов, которые могут стать основой для будущих исследований (и материалом для раздела обсуждения вашей статьи). Дэрил Бем (2003) предполагает, что вы

[e]изучите [ваши данные] со всех сторон. Проанализируйте пол отдельно. Составьте новые составные индексы. Если данные предполагают новую гипотезу, попытайтесь найти дополнительные доказательства в других местах данных. Если вы видите смутные следы интересных закономерностей, попробуйте реорганизовать данные, чтобы сделать их более рельефными. Если есть участники, которые вам не нравятся, или испытания, наблюдатели или интервьюеры, которые дали вам аномальные результаты, исключите их (временно). Отправляйтесь на рыбалку за чем-нибудь — чем угодно — интересным. (стр. 186–187) Бем, DJ (2003). Написание статьи для эмпирического журнала. В JM Darley, MP Zanna и HL Roediger III (Eds.), The compleat Academic: A Career Guide (2-е изд., стр. 185–219). Вашингтон, округ Колумбия: Американская психологическая ассоциация.

Однако важно быть осторожным, потому что сложные наборы данных, скорее всего, будут включать «паттерны», возникшие совершенно случайно. Таким образом, результаты, обнаруженные во время «рыбалки», должны быть воспроизведены по крайней мере в одном новом исследовании, прежде чем они будут представлены как самостоятельные новые явления.

Поймите свою описательную статистику

В следующей главе мы рассмотрим статистику логического вывода — набор методов, позволяющих решить, применимы ли результаты вашей выборки к генеральной совокупности. Хотя статистика выводов важна по причинам, которые мы вскоре объясним, начинающие исследователи иногда забывают, что их описательная статистика действительно говорит о том, «что произошло» в их исследовании. Например, представьте, что группа лечения из 50 участников имеет средний балл 34,32 ( SD = 10,45), контрольная группа из 50 участников имеет средний балл 21,45 ( SD = 9,22), а d Коэна составляет чрезвычайно сильное значение 1,31. Хотя проведение и отчетность по статистике логического вывода (например, ттест), безусловно, будет обязательной частью любого официального отчета об этом исследовании, из одной только описательной статистики должно быть ясно, что лечение работает. Или представьте, что диаграмма рассеяния показывает нечеткое «облако» точек, а r Пирсона равно тривиальному —0,02. Опять же, несмотря на то, что проведение и отчетность по логической статистике были бы обязательной частью любого официального отчета об этом исследовании, из одной только описательной статистики должно быть ясно, что переменные по существу не связаны между собой. Дело в том, что вы всегда должны быть уверены, что сначала полностью понимаете свои результаты на описательном уровне, а затем переходите к выводной статистике.

КЛЮЧЕВЫЕ ВЫВОДЫ

• Необработанные данные необходимо подготовить для анализа, проверив их на наличие возможных ошибок, упорядочив их и введя в программу электронных таблиц.
• Предварительный анализ любого набора данных включает проверку надежности мер, оценку эффективности любых манипуляций, изучение распределений отдельных переменных и выявление выбросов.
• Выбросы, которые кажутся результатом ошибки, непонимания или недостатка усилий, могут быть исключены из анализа. Критерии исключенных ответов или участников должны применяться одинаково ко всем данным и описываться при представлении результатов. Исключенные данные следует откладывать, а не уничтожать или удалять на случай, если они потребуются позже.
• Описательная статистика рассказывает историю того, что произошло в исследовании. Хотя выводная статистика также важна, важно сначала понять описательную статистику.

УПРАЖНЕНИЕ

1. Обсуждение: Каковы по крайней мере два разумных способа справиться с каждым из следующих выбросов на основе обсуждения в этой главе? (a) Участник, оценивающий рост обычных людей, оценивает рост одной женщины как «84 дюйма». (б) В исследовании памяти на обычные объекты один участник набрал 0 баллов из 15. (в) В ответ на вопрос о том, сколько у него «близких друзей», один участник пишет «32».