сайты для фриланса

 

studwork   Заработок на написании научных работ.  Зарабатывайте на сайте фриланса ежедневно.

биржа ссылок    http://www.rotapost.ru/ 

биржа фриланса https://kwork.ru 

 Биржа консалтинга https://www.liveexpert.ru

Купить хостинг домен    ukraine.com.ua

биржа ссылок рекламы    blogun 

платежная система для фрилансеров capitalist 

Купить книгу " форекс основы " электронная версия, цена 2 доллара

Купить книгу " фото городов США " электронная версия, цена 2 доллара

Купить книгу " 1000 бизнес- идей " электронная версия, цена 2 доллара

Купить книгу "Золотые правила общения" электронная версия, цена 2 доллара

Купить емейл базу 500 000 адресов, пишите на почту

написать по вопросу покупки  

toshatereh@gmail.com   ИЛИ  aarci4772@gmail.com

 Напишите на почту - e - mail,  

Вам дадут реквизиты для оплаты и получите книгу в онлайн формате

 

 

 

Выведенный статистика

Напомним, что Матиас Мель и его коллеги в своем исследовании половых различий в разговорчивости обнаружили, что женщины в их выборке произносили в среднем 16 215 слов в день, а мужчины — в среднем 15 669 слов в день (Мель, Вазире, Рамирес-Эспарса). , Слэтчер и Пеннебейкер, 2007 г.). Мел, М.Р., Вазире, С., Рамирес-Эспарса, Н., Слэтчер, Р.Б., и Пеннебейкер, Дж.В. (2007). Действительно ли женщины более разговорчивы, чем мужчины? Наука , 317 , 82.Но, несмотря на эти половые различия в их выборке, они пришли к выводу, что не было доказательств половых различий в разговорчивости среди населения. Вспомним также, что Аллен Каннер и его коллеги, изучая взаимосвязь между ежедневными неприятностями и симптомами, обнаружили в своей выборке корреляцию +0,60 (Kanner, Coyne, Schaefer, & Lazarus, 1981). Каннер, А. Д., Койн, Дж. К., Шефер, К., и Лазарус, Р. С. (1981). Сравнение двух режимов измерения стресса: ежедневные неприятности и подъемы по сравнению с крупными жизненными событиями. Журнал поведенческой медицины , 4 , 1–39. Но они пришли к выводу, что это означает , чтовзаимосвязь между неприятностями и симптомами в популяции. Это поднимает вопрос о том, как исследователи могут сказать, отражает ли результат их выборки что-то, что верно для населения.

Ответ на этот вопрос заключается в том, что они используют набор методов, называемых статистикой вывода, о чем и пойдет речь в этой главе. Мы сосредоточимся, в частности, на проверке нулевой гипотезы, наиболее распространенном подходе к выводной статистике в психологических исследованиях. Мы начнем с концептуального обзора проверки нулевой гипотезы, включая ее цель и основную логику. Затем мы рассмотрим несколько методов проверки нулевой гипотезы, чтобы сделать выводы о различиях между средними значениями и о корреляциях между количественными переменными. Наконец, мы рассмотрим несколько других важных идей, связанных с проверкой нулевой гипотезы, включая те, которые могут быть полезны при планировании новых исследований и интерпретации результатов. Мы также рассмотрим некоторые давние критические замечания в отношении проверки нулевых гипотез и некоторые способы борьбы с этими критическими замечаниями.

13.1 Понимание проверки нулевой гипотезы

ЦЕЛИ ОБУЧЕНИЯ

1. Объясните цель проверки нулевой гипотезы, включая роль ошибки выборки.
2. Опишите базовую логику проверки нулевой гипотезы.
3. Опишите роль силы взаимосвязи и размера выборки в определении статистической значимости и сделайте разумные суждения о статистической значимости на основе этих двух факторов.

Цель проверки нулевой гипотезы

Как мы видели, психологические исследования обычно включают измерение одной или нескольких переменных для выборки и вычисление описательной статистики для этой выборки. Однако в целом цель исследователя состоит не в том, чтобы сделать выводы об этой выборке, а в том, чтобы сделать выводы о совокупности, из которой была отобрана выборка. Таким образом, исследователи должны использовать выборочную статистику, чтобы сделать выводы о соответствующих значениях в популяции. Эти соответствующие значения в совокупности называются параметрами. Представьте, например, что исследователь измеряет количество симптомов депрессии у каждого из 50 взрослых с клинической депрессией и вычисляет среднее количество симптомов. Исследователь, вероятно, хочет использовать эту выборочную статистику (среднее количество симптомов для выборки), чтобы сделать выводы о соответствующем параметре популяции (среднее количество симптомов у взрослых с клинической депрессией).

К сожалению, выборочная статистика не является идеальной оценкой соответствующих параметров совокупности. Это связано с тем, что существует определенная доля случайной изменчивости в любой статистике от выборки к выборке. Среднее количество депрессивных симптомов может быть 8,73 в одной выборке взрослых с клинической депрессией, 6,45 во второй выборке и 9,44 в третьей, даже если эти выборки выбраны случайным образом из одной и той же популяции. Точно так же корреляция ( r Пирсона ) между двумя переменными может составлять +,24 в одной выборке, -0,04 во второй выборке и +,15 в третьей — опять же, даже если эти выборки выбираются случайным образом из одной и той же совокупности. Эта случайная изменчивость статистики от выборки к выборке называется ошибкой выборки . (Обратите внимание, что термин ошибказдесь относится к случайной изменчивости и не означает, что кто-то сделал ошибку. Никто не «совершает ошибку выборки».)

Одним из следствий этого является то, что при наличии статистической взаимосвязи в выборке не всегда ясно, существует ли статистическая взаимосвязь в генеральной совокупности. Небольшая разница между средними значениями двух групп в выборке может указывать на наличие небольшой разницы между средними значениями двух групп в совокупности. Но также может быть так, что между средними значениями в генеральной совокупности нет разницы, а разница в выборке — это всего лишь ошибка выборки. Точно так же значение r Пирсона, равное -0,29 в выборке, может означать, что в популяции существует отрицательная связь. Но также может быть и так, что в популяции нет связи, а связь в выборке — это всего лишь ошибка выборки.

Фактически любую статистическую связь в выборке можно интерпретировать двояко:

1. В популяции существует связь, и связь в выборке это отражает.
2. В генеральной совокупности связи нет, а связь в выборке отражает только ошибку выборки.

Цель проверки нулевой гипотезы — просто помочь исследователям сделать выбор между этими двумя интерпретациями.

Логика проверки нулевой гипотезы

Проверка нулевой гипотезы — это формальный подход к выбору между двумя интерпретациями статистической взаимосвязи в выборке. Одна интерпретация называется нулевой гипотезой (часто обозначается символом H ₀ и читается как «H-ноль»). Это идея о том, что в генеральной совокупности нет взаимосвязи и что взаимосвязь в выборке отражает только ошибку выборки. Неформально нулевая гипотеза состоит в том, что выборочные отношения «возникли случайно». Другая интерпретация называется альтернативной гипотезой (часто обозначаемой как H ₁ ). Это идея о том, что в популяции существует взаимосвязь и что взаимосвязь в выборке отражает эту взаимосвязь в популяции.

Опять же, каждое статистическое отношение в выборке можно интерпретировать одним из следующих двух способов: оно могло возникнуть случайно или могло отражать отношение в популяции. Поэтому исследователям нужен способ сделать выбор между ними. Хотя существует множество конкретных методов проверки нулевой гипотезы, все они основаны на одной и той же общей логике. Шаги следующие:

1. Предположим на данный момент, что нулевая гипотеза верна. Между переменными в популяции нет связи.
2. Определите, насколько вероятными были бы выборочные отношения, если бы нулевая гипотеза была верна.
3. Если выборочная взаимосвязь крайне маловероятна, отклоните нулевую гипотезу в пользу альтернативной гипотезы. Если это не будет крайне маловероятным, то сохраните нулевую гипотезу .

Следуя этой логике, мы можем начать понимать, почему Мель и его коллеги пришли к выводу, что в популяции нет разницы в разговорчивости между женщинами и мужчинами. По сути, они задавали следующий вопрос: «Если бы не было различий в популяции, насколько вероятно, что мы нашли бы небольшую разницу d?= 0,06 в нашей выборке?» Их ответ на этот вопрос заключался в том, что эта выборочная связь была бы достаточно вероятной, если бы нулевая гипотеза была верна. Поэтому они сохранили нулевую гипотезу, сделав вывод об отсутствии доказательств половых различий в популяции. Мы также можем понять, почему Каннер и его коллеги пришли к выводу, что существует корреляция между неприятностями и симптомами среди населения. Они спросили: «Если нулевая гипотеза верна, насколько вероятно, что мы обнаружим сильную корреляцию +,60 в нашей выборке?» Их ответ на этот вопрос заключался в том, что эта выборочная связь была бы довольно маловероятной, если бы нулевая гипотеза была верна. Поэтому они отклонили нулевую гипотезу в пользу альтернативной гипотезы, сделав вывод о наличии положительной корреляции между этими переменными в популяции.

Важным шагом в проверке нулевой гипотезы является определение вероятности результата выборки, если нулевая гипотеза верна. Эта вероятность называется значением p . Низкое значение p означает, что результат выборки был бы маловероятным, если бы нулевая гипотеза была верна, и приводит к отклонению нулевой гипотезы. Высокое значение p означает, что результат выборки был бы вероятным, если бы нулевая гипотеза была верна, и приводит к сохранению нулевой гипотезы. Но насколько низким должно быть значение p , чтобы результат выборки считался достаточно маловероятным, чтобы отвергнуть нулевую гипотезу? При проверке нулевой гипотезы этот критерий называется α (альфа)и почти всегда устанавливается на 0,05. Если вероятность того, что результат будет таким же экстремальным, как результат выборки, составляет менее 5%, если нулевая гипотеза верна, то нулевая гипотеза отклоняется. Когда это происходит, говорят, что результат является статистически значимым . Если вероятность того, что нулевая гипотеза верна, составляет более 5%, что результат будет таким же экстремальным, как и результат выборки, нулевая гипотеза сохраняется. Это не обязательно означает, что исследователь принимает нулевую гипотезу как истинную — только то, что в настоящее время недостаточно доказательств, чтобы сделать вывод, что она верна. Исследователи часто используют выражение «не отвергнуть нулевую гипотезу», а не «сохранить нулевую гипотезу», но они никогда не используют выражение «принять нулевую гипотезу».

Неправильно понятое значение p

Величина р — одна из самых неправильно понимаемых величин в психологических исследованиях (Cohen, 1994). Коэн, Дж. (1994). Мир круглый: p < 0,05. Американский психолог, 49 , 997–1003. Даже профессиональные исследователи неверно истолковывают его, и нередко такие неверные толкования появляются в учебниках по статистике!

Наиболее распространенное неправильное истолкование состоит в том, что значение p — это вероятность того, что нулевая гипотеза верна, то есть результат выборки появился случайно. Например, заблуждающийся исследователь может сказать, что, поскольку значение p равно 0,02, вероятность того, что результат получен случайно, составляет всего 2%, а вероятность того, что он отражает реальные отношения в популяции, составляет 98%. Но это неправильно . Значение p на самом деле представляет собой вероятность результата, по крайней мере столь же экстремального, как результат выборки , если бы нулевая гипотеза была верна. Таким образом, значение p , равное 0,02, означает, что если бы нулевая гипотеза была верна, такой экстремальный результат выборки возник бы только в 2% случаев.

Вы можете избежать этого недоразумения, если вспомните, что значение p не является вероятностью того, что какая-либо конкретная гипотеза верна или ложна. Вместо этого это вероятность получения результата выборки , если нулевая гипотеза верна.

Роль размера выборки и силы связи

Напомним, что проверка нулевой гипотезы включает в себя ответ на вопрос: «Если нулевая гипотеза верна, какова вероятность того, что выборка окажется столь же экстремальной?» Другими словами, «Каково значение p ?» Может быть полезно увидеть, что ответ на этот вопрос зависит всего от двух соображений: силы связи и размера выборки. В частности, чем сильнее выборочная связь и чем больше выборка, тем менее вероятным будет результат, если нулевая гипотеза верна. То есть, чем ниже значение p . Это должно иметь смысл. Представьте себе исследование, в котором выборка из 500 женщин сравнивается с выборкой из 500 мужчин с точки зрения какой-либо психологической характеристики, и d Коэнасильный 0,50. Если бы в популяции действительно не было половых различий, то такой сильный результат, основанный на такой большой выборке, должен казаться маловероятным. Теперь представьте себе аналогичное исследование, в котором выборка из трех женщин сравнивается с выборкой из трех мужчин, и d Коэна составляет слабое значение 0,10. Если бы в популяции не было половых различий, то такая слабая связь, основанная на такой небольшой выборке, должна казаться вероятной. И именно поэтому нулевая гипотеза будет отвергнута в первом примере и сохранена во втором.

Конечно, иногда результат может быть слабым, а выборка большой, или результат может быть сильным, а выборка маленькой. В этих случаях два соображения компенсируют друг друга, так что слабый результат может быть статистически значимым, если выборка достаточно велика, а сильная связь может быть статистически значимой, даже если выборка мала. Таблица 13.1 «Как сила связи и размер выборки в сочетании определяют, является ли результат статистически значимым»примерно показывает, как сочетаются сила связи и размер выборки, чтобы определить, является ли результат выборки статистически значимым. Столбцы таблицы представляют три уровня силы отношений: слабый, средний и сильный. Строки представляют четыре размера выборки, которые можно считать малыми, средними, большими и очень большими в контексте психологических исследований. Таким образом, каждая ячейка в таблице представляет собой сочетание силы связи и размера выборки. Если ячейка содержит слово Yes , то эта комбинация будет статистически значимой как для d Коэна, так и для r Пирсона . Если оно содержит слово « Нет », то оно не будет статистически значимым ни для одного из них. Есть одна ячейка, где решение для dи r будет другим, а также другим, где оно может отличаться в зависимости от некоторых дополнительных соображений, которые обсуждаются в Разделе 13.2 «Некоторые основные тесты нулевой гипотезы».

Таблица 13.1. Сочетание силы связи и размера выборки для определения того, является ли результат статистически значимым

	Сила отношений
Размер образца	Слабый	Середина	Сильный
Малый ( N = 20)	Нет	Нет	д = может быть р = Да
Средний ( N = 50)	Нет	Да	Да
Большой ( N = 100)	д = да р = нет	Да	Да
Очень большой ( N = 500)	Да	Да	Да

Хотя Таблица 13.1 «Как сила связи и размер выборки сочетаются для определения того, является ли результат статистически значимым»дает только приблизительное руководство, оно очень ясно показывает, что слабые связи, основанные на средних или малых выборках, никогда не бывают статистически значимыми, а сильные связи, основанные на средних или больших выборках, всегда статистически значимы. Если вы будете помнить об этом, вы часто будете знать, является ли результат статистически значимым, основываясь только на описательной статистике. Чрезвычайно полезно иметь возможность развивать такого рода интуитивное суждение. Одна из причин заключается в том, что это позволяет вам формировать ожидания относительно того, какими будут результаты ваших формальных тестов нулевой гипотезы, что, в свою очередь, позволяет вам обнаруживать проблемы в ваших анализах. Например, если ваша выборочная взаимосвязь сильная, а ваша выборка средняя, ​​вы должны отклонить нулевую гипотезу. Если по какой-то причине ваш формальный тест нулевой гипотезы указывает на обратное, тогда вам нужно перепроверить свои расчеты и интерпретации. Вторая причина заключается в том, что способность делать такого рода интуитивные суждения указывает на то, что вы понимаете основную логику этого подхода в дополнение к способности выполнять вычисления.

Статистическая значимость против практической значимости

Таблица 13.1 «Как сила связи и размер выборки сочетаются для определения того, является ли результат статистически значимым» иллюстрирует еще один чрезвычайно важный момент. Статистически значимый результат не обязательно является сильным. Даже очень слабый результат может быть статистически значимым, если он основан на достаточно большой выборке. Это тесно связано с аргументом Джанет Шибли Хайд о половых различиях (Hyde, 2007). Хайд, Дж. С. (2007). Новые направления в изучении гендерных сходств и различий. Текущие направления в психологической науке , 16 , 259–263. Различия между женщинами и мужчинами в решении математических задач и лидерских способностях статистически значимы. Но слово значимоеможет заставить людей интерпретировать эти различия как сильные и важные — возможно, даже достаточно важные, чтобы влиять на курсы колледжа, которые они выбирают, или даже на то, за кого они голосуют. Однако, как мы видели, эти статистически значимые различия на самом деле весьма слабы — возможно, даже «тривиальны».

Вот почему важно различать статистическую значимость результата и практическую значимость этого результата. Практическая значимостьотносится к важности или полезности результата в некотором реальном контексте. Многие половые различия статистически значимы и даже могут представлять интерес с чисто научной точки зрения, но они не имеют практического значения. В клинической практике это же понятие часто называют «клинической значимостью». Например, исследование нового метода лечения социальной фобии может показать, что он дает статистически значимый положительный эффект. Тем не менее, этот эффект все еще может быть недостаточно сильным, чтобы оправдать время, усилия и другие затраты на его применение на практике, особенно если более простые и дешевые методы лечения, которые работают почти так же хорошо, уже существуют. Хотя этот результат является статистически значимым, можно сказать, что он не имеет практического или клинического значения.

КЛЮЧЕВЫЕ ВЫВОДЫ

• Проверка нулевой гипотезы — это формальный подход к решению вопроса о том, отражает ли статистическая взаимосвязь в выборке реальную взаимосвязь в популяции или это просто случайность.
• Логика проверки нулевой гипотезы включает в себя предположение, что нулевая гипотеза верна, определение того, насколько вероятным был бы результат выборки, если бы это предположение было правильным, а затем принятие решения. Если результат выборки был бы маловероятным, если бы нулевая гипотеза была верна, то он отклоняется в пользу альтернативной гипотезы. Если это не маловероятно, то нулевая гипотеза сохраняется.
• Вероятность получения результата выборки, если нулевая гипотеза верна ( значение p ), основана на двух соображениях: силе связи и размере выборки. Разумные суждения о том, являются ли выборочные отношения статистически значимыми, часто можно сделать, быстро рассмотрев эти два фактора.
• Статистическая значимость — это не то же самое, что сила или важность отношений. Даже слабые отношения могут быть статистически значимыми, если размер выборки достаточно велик. Важно учитывать силу связи и практическую значимость результата в дополнение к его статистической значимости.

УПРАЖНЕНИЯ

1. Обсуждение: представьте себе исследование, показывающее, что люди, которые едят больше брокколи, как правило, счастливее. Объясните человеку, ничего не смыслящему в статистике, зачем исследователи проводят проверку нулевой гипотезы.

2. Практика: Используйте Таблицу 13.1 «Как сила связи и размер выборки сочетаются для определения того, является ли результат статистически значимым» , чтобы решить, является ли каждый из следующих результатов статистически значимым.

   1. Корреляция между двумя переменными составляет r = -0,78 на основе размера выборки 137.
   2. Средний балл по психологической характеристике для женщин составляет 25 ( SD = 5), а средний балл для мужчин — 24 ( SD = 5). В исследовании приняли участие 12 женщин и 10 мужчин.
   3. В эксперименте на память среднее количество элементов, которое вспомнили 40 участников в состоянии А, было на 0,50 стандартного отклонения больше, чем среднее число, которое вспомнили 40 участников в состоянии Б.
   4. В другом эксперименте с памятью средние баллы участников в условиях А и В оказались абсолютно одинаковыми!
   5. Учащийся находит корреляцию r = 0,04 между количеством единиц, которые учащиеся изучают в его классе методов исследования, и уровнем стресса учащихся.

13.2 Некоторые основные тесты нулевой гипотезы

ЦЕЛИ ОБУЧЕНИЯ

1. Проведение и интерпретация одновыборочных, зависимых и независимых выборок t - тестов.
2. Интерпретируйте результаты односторонних, повторных измерений и факторного ANOVA.
3. Проведите и интерпретируйте тесты нулевой гипотезы r Пирсона .

В этом разделе мы рассмотрим несколько распространенных процедур проверки нулевой гипотезы. Акцент здесь делается на предоставлении достаточного количества информации, чтобы позволить вам проводить и интерпретировать самые основные версии. В большинстве случаев онлайн-инструменты статистического анализа, упомянутые в главе 12 «Описательная статистика» , справятся с вычислениями, как и такие программы, как Microsoft Excel и SPSS.

Т - тест

Как мы видели на протяжении всей этой книги, многие исследования в области психологии сосредоточены на различии между двумя средствами. Наиболее распространенным тестом нулевой гипотезы для этого типа статистической взаимосвязи является t - критерий . В этом разделе мы рассмотрим три типа t -критерия, которые используются для несколько разных планов исследования: t-критерий для одной выборки , t - критерий для зависимых выборок и t - критерий для независимых выборок .

Одновыборочный t - критерий

Одновыборочный t - критерий используется для сравнения среднего значения выборки ( M ) с гипотетическим средним значением совокупности (μ ₀ ), что обеспечивает некоторый интересный стандарт сравнения. Нулевая гипотеза состоит в том, что среднее значение для совокупности (µ) равно гипотетическому среднему значению для совокупности: µ = µ ₀ . Альтернативная гипотеза состоит в том, что среднее значение для совокупности отличается от гипотетического среднего значения для совокупности: μ _≠ μ ₀ . Чтобы сделать выбор между этими двумя гипотезами, нам нужно найти вероятность получения выборочного среднего (или еще одного экстремального), если нулевая гипотеза верна. Но для нахождения этого значения p требуется сначала вычислить тестовую статистику, называемую t .. ( Тестовая статистика — это статистика, которая вычисляется только для того, чтобы помочь найти значение p .) Формула для t выглядит следующим образом:

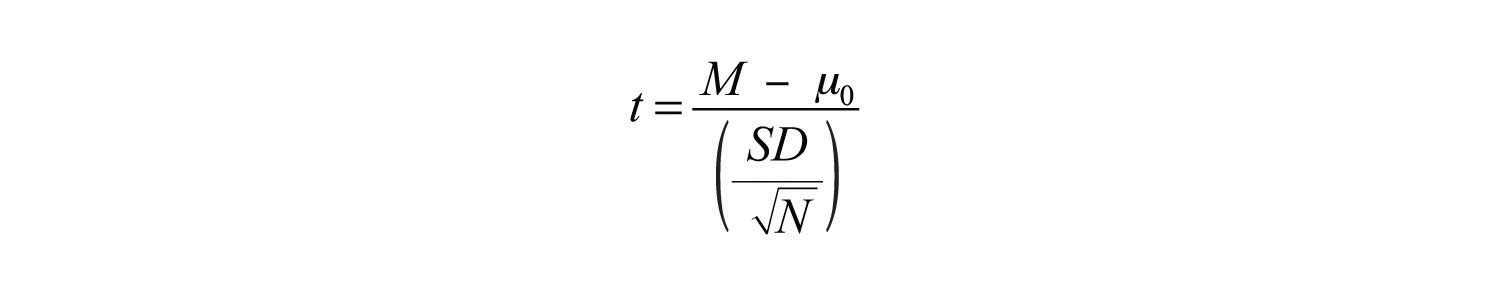
Опять же, M — выборочное среднее, а µ ₀ — гипотетическое среднее интересующей совокупности. SD — это стандартное отклонение выборки, а N — размер выборки.

Причина, по которой t - статистика (или любая тестовая статистика) полезна, заключается в том, что мы знаем, как она распределяется, когда нулевая гипотеза верна. Как показано на рис. 13.1 «Распределение» , это распределение унимодальное и симметричное, а его среднее значение равно 0. Его точная форма зависит от статистического понятия, называемого степенями свободы, которые для одновыборочного t - критерия равны N — 1. (Существует 24 степени свободы для распределения, показанного на рис. 13.1 «Распределение» .) Важным моментом является то, что знание этого распределения позволяет найти значение p для любого показателя t . Рассмотрим, например, тбалл +1,50 на основе выборки из 25. Вероятность t - балла, по крайней мере, этого экстремального значения определяется долей t - баллов в распределении, которые являются, по крайней мере, этим экстремальным. А пока давайте определим экстремум как далекий от нуля в любом направлении. Таким образом, значение p представляет собой долю t - показателей, которые составляют +1,50 или выше или -1,50 или ниже — значение, которое оказывается равным 0,14.

Рис. 13.1 Распределение t - оценок (с 24 степенями свободы), когда нулевая гипотеза верна

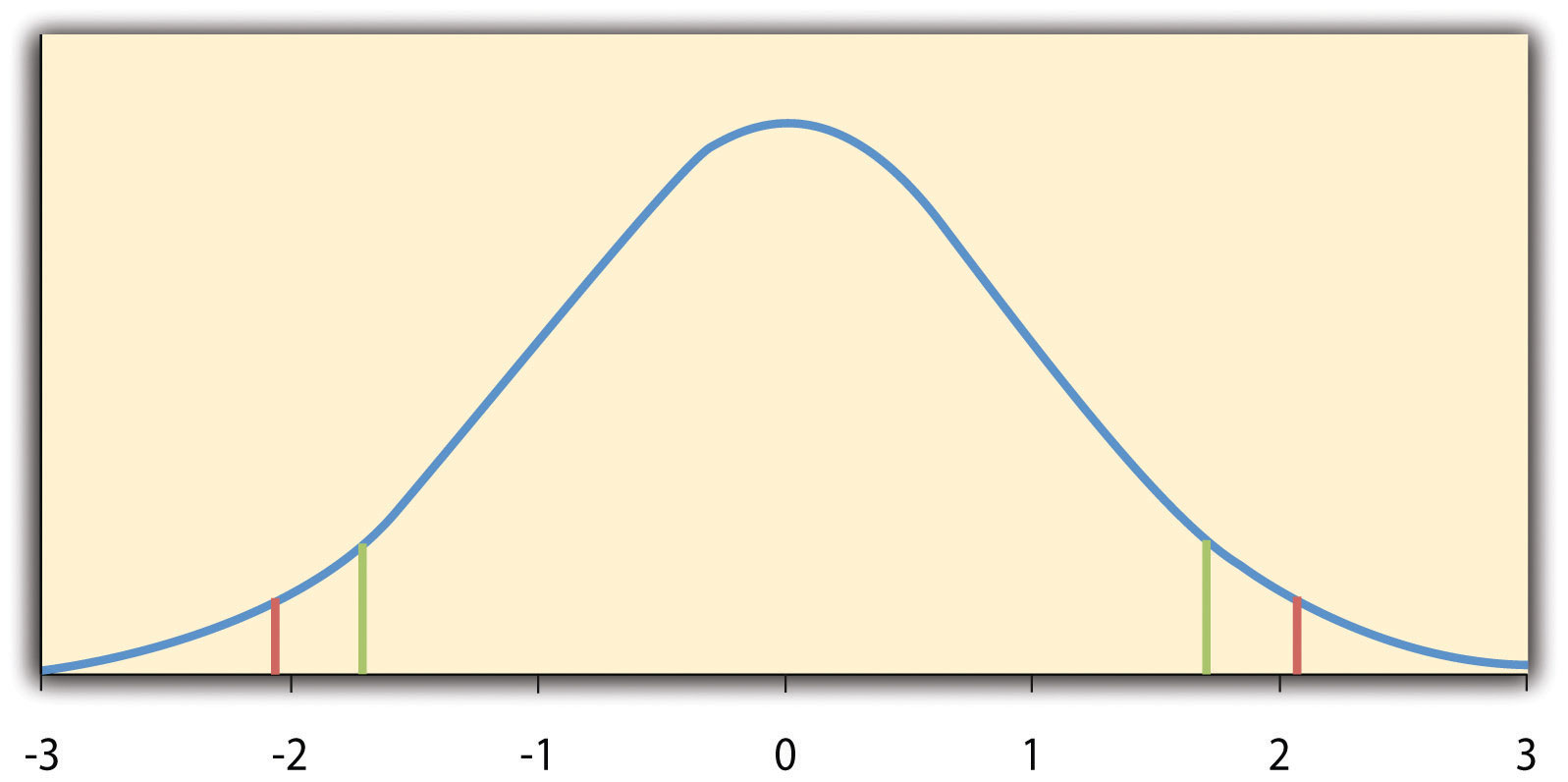
Красные вертикальные линии представляют двусторонние критические значения, а зеленые вертикальные линии — односторонние критические значения при α = 0,05.

К счастью, нам не нужно иметь дело непосредственно с распределением t - показателей. Если бы мы ввели наши выборочные данные и гипотетическое среднее интереса в один из статистических онлайн-инструментов в главе 12 «Описательная статистика» или в такую ​​программу, как SPSS (в Excel нет функции одновыборочного t - теста), результат был бы таким: включают как t - показатель, так и значение p . На этом этапе остальная часть процедуры проста. Если p меньше 0,05, мы отклоняем нулевую гипотезу и делаем вывод, что среднее значение генеральной совокупности отличается от гипотетического среднего интереса. Если рбольше 0,05, мы сохраняем нулевую гипотезу и заключаем, что недостаточно доказательств, чтобы сказать, что среднее значение генеральной совокупности отличается от гипотетического среднего интереса. (Опять же, технически мы заключаем только, что у нас недостаточно доказательств, чтобы заключить, что оно действительно отличается.)

Если бы нам нужно было вычислить показатель t вручную, мы могли бы использовать для принятия решения таблицу, подобную таблице 13.2 «Таблица критических значений» . В этой таблице не указаны фактические значения p . Вместо этого он предоставляет критические значения t для различных степеней свободы ( df) , когда α равно 0,05. А пока давайте сосредоточимся на двухсторонних критических значениях в последнем столбце таблицы. Каждое из этих значений следует интерпретировать как пару значений: одно положительное и одно отрицательное. Например, двусторонние критические значения при 24 степенях свободы составляют +2,064 и -2,064. Они представлены красными вертикальными линиями на рис. 13.1 «Распределение».. Идея состоит в том, что любой t -показатель ниже нижнего критического значения (левая красная линия на рис. 13.1 «Распределение» ) относится к нижним 2,5% распределения, в то время как любой t -показатель выше верхнего критического значения (правая ручная красная линия) находится в верхних 2,5% распределения. Это означает, что любая t -оценка, превышающая критическое значение в любом направлении, находится в самых крайних 5% t - оценок, когда нулевая гипотеза верна, и, следовательно, имеет значение p менее 0,05. Таким образом, если вычисляемый нами показатель t превышает критическое значение в любом направлении, мы отклоняем нулевую гипотезу. Если тоценка, которую мы вычисляем, находится между верхним и нижним критическими значениями, тогда мы сохраняем нулевую гипотезу.

Таблица 13.2 Таблица критических значений t при α = 0,05

	Критическое значение
дф	Однохвостый	Двухвостый
3	2,353	3.182
4	2.132	2,776
5	2,015	2,571
6	1,943	2,447
7	1,895	2,365
8	1.860	2.306
9	1,833	2,262
10	1,812	2,228
11	1,796	2.201
12	1,782	2,179
13	1,771	2.160
14	1,761	2,145
15	1,753	2.131
16	1,746	2.120
17	1.740	2.110
18	1,734	2.101
19	1,729	2.093
20	1,725	2.086
21	1,721	2.080
22	1,717	2.074
23	1,714	2,069
24	1,711	2.064
25	1,708	2.060
30	1,697	2.042
35	1.690	2.030
40	1,684	2.021
45	1,679	2,014
50	1,676	2.009
60	1,671	2.000
70	1,667	1,994
80	1,664	1.990
90	1,662	1,987
100	1,660	1,984

До сих пор мы рассматривали так называемый двусторонний тест , в котором мы отклоняем нулевую гипотезу, если показатель t для выборки является экстремальным в любом направлении. Это имеет смысл, когда мы считаем, что среднее значение выборки может отличаться от гипотетического среднего значения генеральной совокупности, но у нас нет веских оснований ожидать, что эта разница пойдет в определенном направлении. Но также можно выполнить односторонний тест , в котором мы отклоняем нулевую гипотезу только в том случае, если показатель t для выборки является экстремальным в одном направлении, которое мы указываем перед сбором данных. Это имеет смысл, когда у нас есть веские основания ожидать, что среднее значение выборки будет отличаться от гипотетического среднего значения генеральной совокупности в определенном направлении.

Вот как это работает. Каждое одностороннее критическое значение в таблице 13.2 «Таблица критических значений» можно снова интерпретировать как пару значений: одно положительное и одно отрицательное. Показатель t ниже нижнего критического значения соответствует 5% самых низких значений распределения, а показатель t выше верхнего критического значения соответствует 5% самых высоких значений распределения. Для 24 степеней свободы эти значения составляют −1,711 и +1,711. (Они представлены зелеными вертикальными линиями на рисунке 13.1 «Распределение».) Однако для одностороннего теста мы должны решить перед сбором данных, ожидаем ли мы, что среднее значение выборки будет ниже, чем среднее значение гипотетической совокупности, и в этом случае мы будем использовать только более низкое критическое значение, или мы ожидаем, что среднее значение выборки быть больше, чем гипотетическое среднее значение населения, и в этом случае мы будем использовать только верхнее критическое значение. Обратите внимание, что мы по-прежнему отклоняем нулевую гипотезу, когда t - показатель для нашей выборки находится в самых крайних 5% t-показателей, которые мы ожидали бы, если бы нулевая гипотеза была верна, поэтому α остается на уровне 0,05. Мы просто переопределили крайниеотноситься только к одному хвосту распределения. Преимущество одностороннего теста состоит в том, что критические значения менее экстремальны. Если среднее значение выборки отличается от гипотетического среднего значения генеральной совокупности в ожидаемом направлении, то у нас больше шансов отклонить нулевую гипотезу. Недостатком является то, что если среднее значение выборки отличается от гипотетического среднего значения генеральной совокупности в неожиданном направлении, то нет никаких шансов отвергнуть нулевую гипотезу.

Пример одновыборочного t - критерия

Представьте, что психолога, занимающегося вопросами здоровья, интересует точность оценки студентов колледжа количества калорий в печенье с шоколадной крошкой. Он показывает печенье выборке из 10 студентов и просит каждого оценить количество калорий в нем. Поскольку фактическое количество калорий в печенье равно 250, это гипотетическое среднее интересующей совокупности (µ ₀ ). Нулевая гипотеза состоит в том, что средняя оценка для населения (μ) равна 250. Поскольку у него нет реального представления о том, будут ли студенты недооценивать или переоценивать количество калорий, он решает провести двусторонний тест. Теперь представьте себе, что фактические оценки участников таковы:

250, 280, 200, 150, 175, 200, 200, 220, 180, 250.

Средняя оценка для образца ( M ) составляет 212,00 калорий, а стандартное отклонение ( SD ) составляет 39,17. Психолог теперь может вычислить t - показатель для своей выборки:

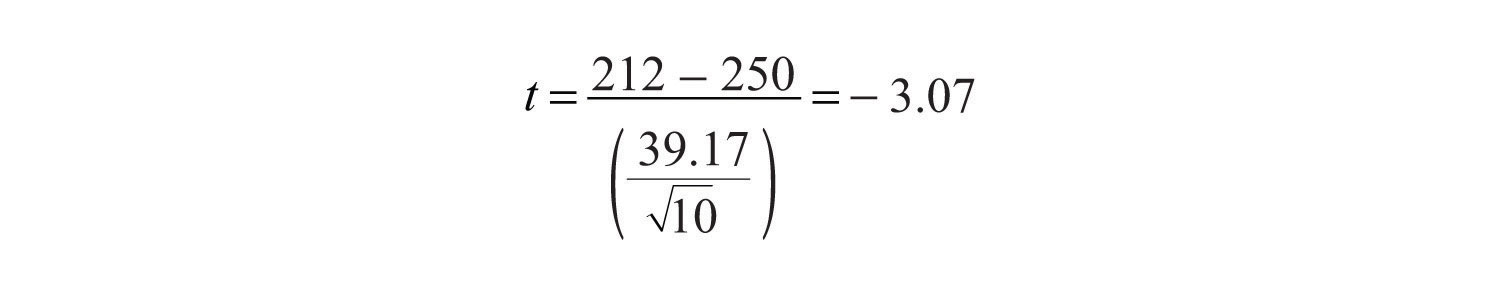
Если он введет данные в один из онлайн-инструментов анализа или воспользуется SPSS, он также сообщит ему, что двустороннее значение p для этого показателя t (с 10 − 1 = 9 степенями свободы) равно 0,013. Поскольку это значение меньше 0,05, психолог в области здравоохранения отклонит нулевую гипотезу и сделает вывод, что студенты колледжей склонны недооценивать количество калорий в печенье с шоколадной крошкой. Если он вычислит показатель t вручную, он может посмотреть в Таблицу 13.2 «Таблица критических значений» и увидеть, что критическое значение t для двустороннего критерия с 9 степенями свободы составляет ±2,262. Тот факт, что его показатель t был более экстремальным, чем это критическое значение, говорил бы ему, что его pзначение меньше 0,05 и что он должен отклонить нулевую гипотезу.

Наконец, если бы этот исследователь приступил к этому исследованию с серьезными основаниями ожидать, что студенты колледжа недооценивают количество калорий, то он мог бы провести односторонний тест вместо двустороннего. Единственное, что это изменит, — это критическое значение, которое будет равно −1,833. Это чуть менее экстремальное значение облегчило бы отклонение нулевой гипотезы. Однако если бы оказалось, что студенты колледжа переоценивают количество калорий — неважно, насколько сильно они его переоценивают, — исследователь не смог бы отвергнуть нулевую гипотезу.

Критерий зависимых выборок t

Критерий зависимых выборок (иногда называемый t - критерием парных выборок ) используется для сравнения двух средних значений для одного и того же образца, протестированного в два разных момента времени или в двух разных условиях . Это делает его подходящим для планов предварительного и последующего тестирования или экспериментов с участием испытуемых. Нулевая гипотеза состоит в том, что средние значения в два раза или при двух условиях одинаковы в популяции. Альтернативная гипотеза состоит в том, что они не одинаковы. Этот тест также может быть односторонним, если у исследователя есть веские основания ожидать, что разница пойдет в определенном направлении.

Это помогает думать о t-критерии зависимых выборок как о частном случае t-критерия одной выборки . Однако первым шагом в t -критерии зависимых выборок является сведение двух оценок каждого участника к единственной разностной оценке путем определения разницы между ними. В этот момент t - критерий зависимых выборок становится одновыборочным t - критерием для оценок различий. Гипотетическое среднее значение популяции (µ ₀ ), представляющее интерес, равно 0, потому что это то, каким был бы показатель средней разности, если бы не было различий в среднем между двумя временами или двумя условиями. Теперь мы можем думать о нулевой гипотезе как о том, что средний показатель разницы в популяции равен 0 (µ₀ = 0), а альтернативная гипотеза заключается в том, что средний балл различия в популяции не равен 0 (µ ₀ ≠ 0).

Пример t -критерия зависимых выборок

Представьте, что медицинский психолог теперь знает, что люди склонны недооценивать количество калорий в нездоровой пище, и разработал короткую программу обучения, чтобы улучшить свои оценки. Чтобы проверить эффективность этой программы, он проводит предварительное и посттестовое исследование, в котором 10 участников оценивают количество калорий в шоколадном печенье перед тренировочной программой, а затем еще раз после нее. Поскольку он ожидает, что программа повысит оценки участников, он решает провести односторонний тест. Теперь представьте себе, что предварительные оценки равны

230, 250, 280, 175, 150, 200, 180, 210, 220, 190

и что посттестовые оценки (для тех же участников в том же порядке)

250, 260, 250, 200, 160, 200, 200, 180, 230, 240.

Таким образом, разница в баллах выглядит следующим образом:

+20, +10, -30, +25, +10, 0, +20, -30, +10, +50.

Обратите внимание, что не имеет значения, вычитается ли первый набор баллов из второго или второй из первого, если это делается одинаково для всех участников. В этом примере имеет смысл вычесть предварительные оценки из посттестовых оценок, чтобы положительные оценки разницы означали, что оценки выросли после обучения, а отрицательные оценки разницы означают, что оценки понизились.

Среднее значение различий составляет 8,50 со стандартным отклонением 27,27. Психолог здоровья теперь может вычислить t - показатель для своей выборки следующим образом:

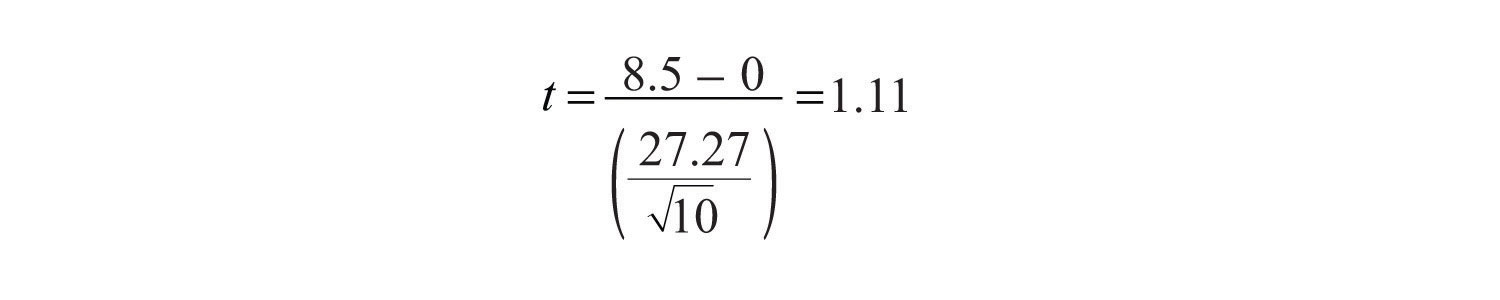
Если он введет данные в один из онлайн-инструментов анализа или воспользуется Excel или SPSS, он сообщит ему, что одностороннее значение p для этого показателя t (опять же с 10 − 1 = 9 степенями свободы) равно 0,148. Поскольку это значение больше 0,05, он оставит нулевую гипотезу и сделает вывод, что тренировочная программа не увеличивает оценку калорийности людей. Если бы ему нужно было вычислить показатель t вручную, он мог бы взглянуть на Таблицу 13.2 «Таблица критических значений» и увидеть, что критическое значение t для одностороннего критерия с 9 степенями свободы равно +1,833. (На этот раз оно положительное, потому что он ожидал получить положительную разницу средних значений.) Тот факт, что его tоценка была менее экстремальной, чем это критическое значение сказало бы ему, что его значение p больше 0,05 и что он не должен отвергать нулевую гипотезу.

Критерий независимых выборок t

Критерий t для независимых выборок используется для сравнения средних значений двух отдельных выборок ( M ₁ и M ₂ ). Две выборки могли быть протестированы в разных условиях в эксперименте между субъектами или они могли быть ранее существовавшими группами в корреляционном плане (например, женщины и мужчины, экстраверты и интроверты). Нулевая гипотеза состоит в том, что средние значения двух совокупностей одинаковы: µ ₁ = µ ₂ . Альтернативная гипотеза состоит в том, что они не совпадают: µ ₁ ≠ µ ₂ . Опять же, тест может быть односторонним, если у исследователя есть веские основания ожидать, что разница пойдет в определенном направлении.

Статистика t здесь немного сложнее, потому что она должна учитывать два средних значения выборки, два стандартных отклонения и два размера выборки. Формула выглядит следующим образом:

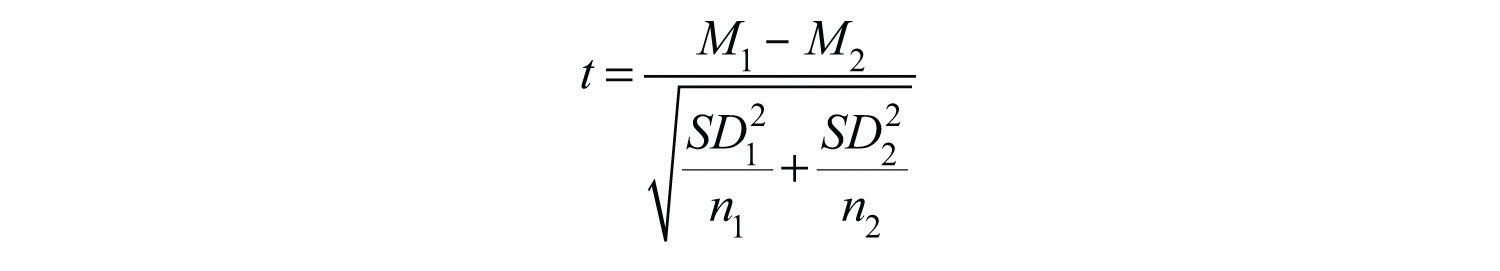
Обратите внимание, что эта формула включает квадраты стандартных отклонений (дисперсии), которые появляются внутри символа квадратного корня. Кроме того, строчные буквы n ₁ и n ₂ относятся к размерам выборки в двух группах или условиях (в отличие от заглавной буквы N , которая обычно относится к общему размеру выборки). Единственная дополнительная вещь, которую нужно знать здесь, это то, что для t - критерия независимых выборок существует N - 2 степени свободы .

Пример t -критерия независимых выборок

Теперь психолог здоровья хочет сравнить оценки калорийности людей, которые регулярно едят нездоровую пищу, с оценками людей, которые редко едят нездоровую пищу. Он считает, что разница может проявляться в любом направлении, поэтому решает провести двусторонний тест. Он собирает данные по выборке из восьми участников, которые регулярно едят нездоровую пищу, и семи участников, которые редко едят нездоровую пищу. Данные следующие:

  

Любители нездоровой пищи: 180, 220, 150, 85, 200, 170, 150, 190

Любители нездоровой пищи: 200, 240, 190, 175, 200, 300, 240

  

Среднее значение для любителей нездоровой пищи составляет 220,71 при стандартном отклонении 41,23. Среднее значение для тех, кто ест нездоровую пищу, составляет 168,12 со стандартным отклонением 42,66. Теперь он может вычислить свой t -показатель следующим образом:

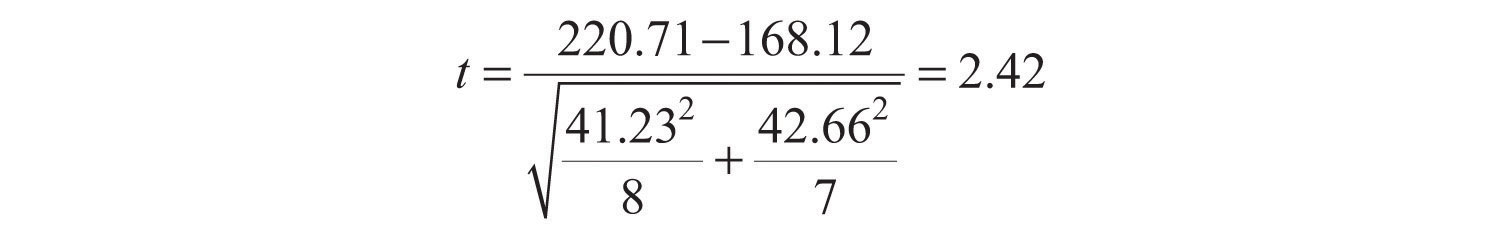
Если он введет данные в один из онлайн-инструментов анализа или воспользуется Excel или SPSS, он сообщит ему, что двустороннее значение p для этого показателя t (с 15 − 2 = 13 степенями свободы) равно 0,015. Поскольку этот показатель меньше 0,05, психолог в области здравоохранения отклонит нулевую гипотезу и сделает вывод, что люди, которые регулярно едят нездоровую пищу, оценивают калорийность ниже, чем люди, которые едят ее редко. Если бы ему нужно было вычислить показатель t вручную, он мог бы взглянуть на Таблицу 13.2 «Таблица критических значений» и увидеть, что критическое значение t для двустороннего критерия с 13 степенями свободы составляет ±2,160. Тот факт, что его показатель t был более экстремальным, чем это критическое значение, говорил бы ему, что егозначение p меньше 0,05 и что он не сможет принять нулевую гипотезу.

Дисперсионный анализ

Когда необходимо сравнить более двух групп или средних условий, наиболее распространенным тестом нулевой гипотезы является дисперсионный анализ (ANOVA) . В этом разделе мы рассмотрим в первую очередь однофакторный дисперсионный анализ , который используется для планов между субъектами с одной независимой переменной. Затем мы кратко рассмотрим некоторые другие версии дисперсионного анализа, которые используются для внутрисубъектных и факторных планов исследования.

Односторонний дисперсионный анализ

Однофакторный дисперсионный анализ используется для сравнения средних значений более чем двух выборок ( M1 , M ₂ … MG ) в _плане между субъектами. Нулевая гипотеза состоит в том, что все средние в популяции равны: µ ₁ = µ ₂ =…= µ _G . Альтернативная гипотеза состоит в том, что не все средства в популяции равны.

Тестовая статистика для ANOVA называется F . Это отношение двух оценок дисперсии генеральной совокупности на основе выборочных данных. Одна оценка дисперсии генеральной совокупности называется средним квадратом между группами ( MS _B ) и основана на различиях между выборочными средними значениями. Другой называется средними квадратами внутри групп ( MSW) и _{основан} на различиях между оценками в каждой группе. Статистика F представляет собой отношение MS _B к MS _W и, следовательно, может быть выражена следующим образом:

$$$$

Опять же, причина полезности F заключается в том, что мы знаем, как она распределяется, когда нулевая гипотеза верна. Как показано на рис. 13.2 «Распределение » , это распределение унимодальное и имеет положительную асимметрию со значениями, которые группируются вокруг 1. Точная форма распределения зависит как от количества групп, так и от размера выборки, и существует несколько степеней свободы. значение, связанное с каждым из них. Межгрупповые степени свободы — это количество групп минус одна: df _B = ( G − 1). Степени свободы внутри групп равны общему объему выборки минус количество групп: df _W = N − G . Опять же, зная распределениеF , когда нулевая гипотеза верна, позволяет нам найти значение p .

Рисунок 13.2 . Распределение отношения F с 2 и 37 степенями свободы, когда нулевая гипотеза верна.

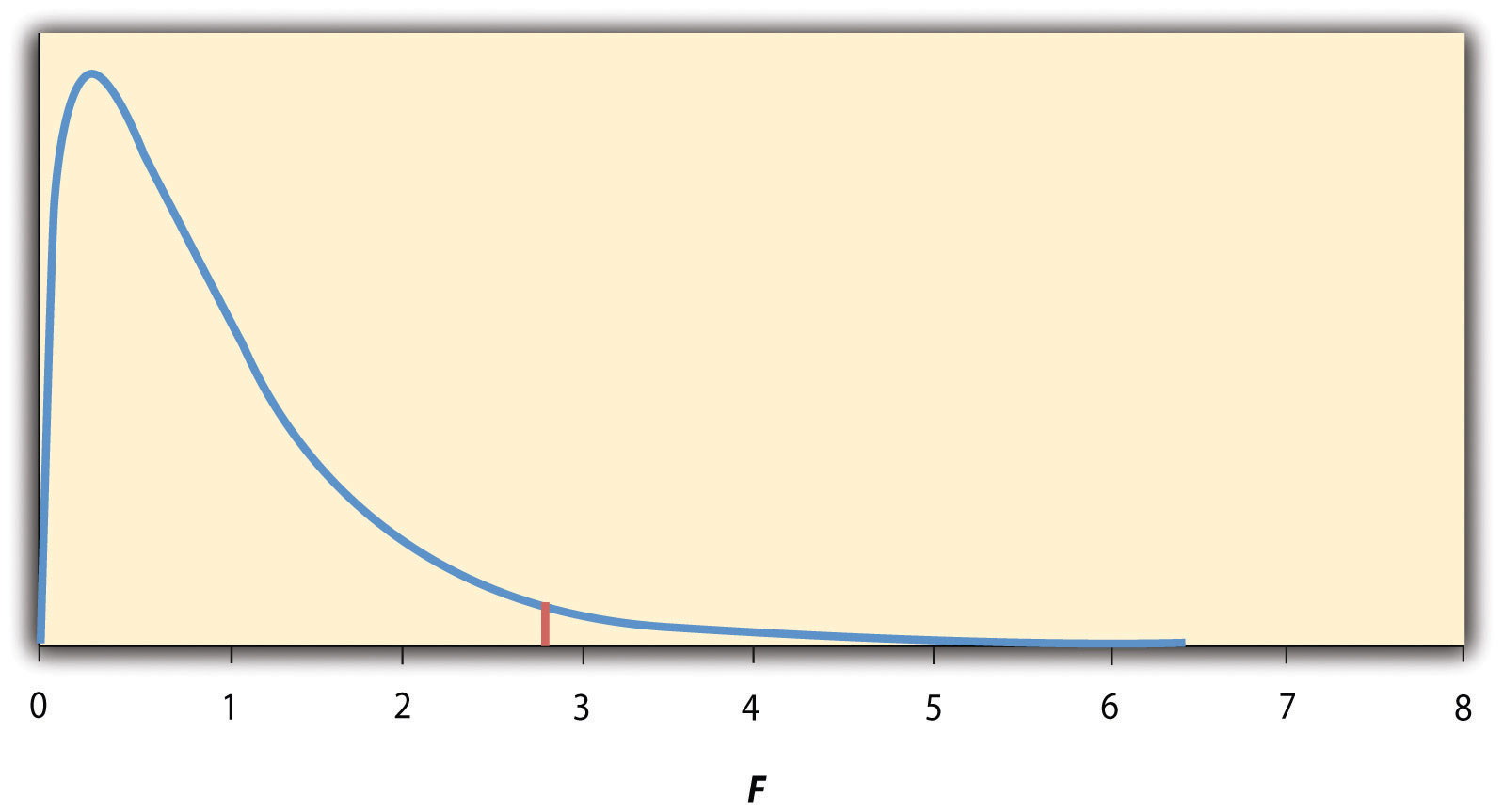
Красная вертикальная линия представляет собой критическое значение, когда α равно 0,05.

Онлайн-инструменты в главе 12 «Описательная статистика» и статистическое программное обеспечение, такое как Excel и SPSS, вычислят F и найдут значение p . Если p меньше 0,05, то мы отклоняем нулевую гипотезу и делаем вывод, что существуют различия между средними значениями групп в популяции. Если p больше 0,05, то мы сохраняем нулевую гипотезу и делаем вывод, что недостаточно доказательств, чтобы сказать, что существуют различия. В том маловероятном случае, если мы будем вычислять F вручную, мы можем использовать для принятия решения таблицу критических значений, подобную Таблице 13.3 «Таблица критических значений» . Идея состоит в том, что любой Fсоотношение выше критического значения имеет значение р менее 0,05. Таким образом, если вычисленное нами отношение F превышает критическое значение, мы отвергаем нулевую гипотезу. Если вычисленное нами отношение F меньше критического значения, то мы сохраняем нулевую гипотезу.

Таблица 13.3 Таблица критических значений F при α = 0,05

дф Б
дф Вт	2	3	4
8	4.459	4.066	3.838
9	4.256	3.863	3,633
10	4.103	3.708	3.478
11	3,982	3,587	3,357
12	3,885	3.490	3.259
13	3.806	3.411	3.179
14	3,739	3.344	3.112
15	3,682	3.287	3.056
16	3,634	3.239	3.007
17	3,592	3.197	2,965
18	3,555	3.160	2,928
19	3.522	3.127	2.895
20	3.493	3.098	2,866
21	3.467	3.072	2.840
22	3.443	3.049	2.817
23	3.422	3.028	2.796
24	3.403	3.009	2,776
25	3,385	2,991	2,759
30	3.316	2,922	2.690
35	3,267	2.874	2,641
40	3.232	2.839	2.606
45	3.204	2.812	2,579
50	3.183	2.790	2,557
55	3,165	2,773	2.540
60	3.150	2,758	2,525
65	3.138	2,746	2,513
70	3.128	2,736	2.503
75	3.119	2,727	2.494
80	3.111	2,719	2,486
85	3.104	2,712	2.479
90	3.098	2.706	2,473
95	3.092	2.700	2,467
100	3.087	2.696	2,463

Пример однофакторного дисперсионного анализа

Представьте, что медицинский психолог хочет сравнить оценки калорийности специалистов по психологии, питанию и профессиональных диетологов. Он собирает следующие данные:

Психологические специальности: 200, 180, 220, 160, 150, 200, 190, 200Специальности по питанию: 190, 220, 200, 230, 160, 150, 200, 210, 195Диетологи: 220, 250, 240, 275, 250, 230, 200, 240

Средние значения составляют 187,50 ( SD = 23,14), 195,00 ( SD = 27,77) и 238,13 ( SD = 22,35) соответственно. Таким образом, получается, что диетологи в среднем сделали значительно более точные оценки. Исследователь почти наверняка введет эти данные в программу, такую ​​как Excel или SPSS, которая вычислит для него F и найдет значение p . В Таблице 13.4 «Типичный однофакторный результат дисперсионного анализа из Excel» показаны выходные данные функции однофакторного дисперсионного анализа в Excel для этих данных. Это называется таблицей ANOVA. Он показывает, что MS _B составляет 5971,88, MS _W составляет 602,23, а их отношение F равно 9,92. р _значение 0,0009. Поскольку это значение ниже 0,05, исследователь отклонил бы нулевую гипотезу и пришел к выводу, что средние оценки калорий для трех групп не совпадают в популяции. Обратите внимание, что таблица ANOVA также включает «сумму квадратов» ( SS ) между группами и внутри групп. Эти значения вычисляются на пути к нахождению MS _B и MS _W , но исследователь обычно не сообщает их. Наконец, если бы исследователь вычислил отношение F вручную, он мог бы посмотреть в Таблицу 13.3 «Таблица критических значений» и увидеть, что критическое значение F с 2 и 21 степенями свободы равно 3,467 (то же самое значение вТабл. 13.4 «Типичный однофакторный результат дисперсионного анализа из Excel» в разделе F _крит ). Тот факт, что его показатель t был более экстремальным, чем это критическое значение, сказал бы ему, что его значение p меньше 0,05 и что он должен отклонить нулевую гипотезу.

Табл. 13.4. Типичные выходные данные однофакторного дисперсионного анализа из Excel

дисперсионный анализ
Источник вариаций	SS	дф	РС	Ф	р-значение	F крит
Между группами	11 943,75	2	5 971 875	9.916234	0,000928	3,4668
Внутри групп	12 646,88	21	602.2321
Общий	24 590,63	23

ANOVA Разработки

Постфактум сравнения

Когда мы отвергаем нулевую гипотезу в однофакторном дисперсионном анализе, мы приходим к выводу, что групповые средние не все одинаковы в популяции. Но это может свидетельствовать о разных вещах. С тремя группами это может указывать на то, что все три средства значительно отличаются друг от друга. Или это может указывать на то, что одно из средств значительно отличается от двух других, но два других существенно не отличаются друг от друга. Например, может случиться так, что средние оценки калорийности специалистов по психологии, питанию и диетологов значительно отличаются друг от друга. Или может случиться так, что средние значения для диетологов значительно отличаются от средних значений для специалистов по психологии и питанию, но средние значения для специалистов по психологии и питанию существенно не отличаются друг от друга. По этой причине,апостериорные сравнения выбранных пар групповых средств для определения того, какие из них отличаются от других.

Одним из подходов к апостериорным сравнениям может быть проведение серии t - критериев для независимых выборок, сравнивающих среднее значение каждой группы со средним значением каждой другой группы. Но есть проблема с этим подходом. В общем, если мы проводим t -тест, когда нулевая гипотеза верна, у нас есть 5%-й шанс ошибочно отвергнуть нулевую гипотезу (см. Раздел 13.3 «Дополнительные соображения» для получения дополнительной информации об ошибках типа I). Если мы проводим несколько t -тестов, когда нулевая гипотеза верна, вероятность ошибочного отклонения хотя бы одной нулевой гипотезы увеличивается с каждым проводимым нами тестом. Таким образом, исследователи обычно не проводят апостериорных сравнений, используя стандартные t.тесты, потому что слишком велика вероятность того, что они ошибочно отклонят хотя бы одну нулевую гипотезу. Вместо этого они используют одну из нескольких модифицированных процедур t -критерия, среди которых процедура Бонферонни, критерий Фишера наименьшей значимой разницы (LSD) и критерий честно значимой разницы Тьюки (HSD). Детали этих подходов выходят за рамки этой книги, но важно понять их назначение. Это необходимо для того, чтобы свести риск ошибочного отклонения истинной нулевой гипотезы к приемлемому уровню (близкому к 5%).

Дисперсионный анализ с повторными измерениями

Напомним, что однофакторный дисперсионный анализ подходит для межсубъектных планов, в которых сравниваемые средние значения исходят от отдельных групп участников. Это не подходит для внутрисубъектных планов, в которых сравниваемые средние значения получены от одних и тех же участников, протестированных в разных условиях или в разное время. Для этого требуется несколько иной подход, называемый дисперсионным анализом с повторными измерениями . Основы дисперсионного анализа с повторными измерениями такие же, как и для однофакторного дисперсионного анализа. Основное отличие состоит в том, что многократное измерение зависимой переменной для каждого участника позволяет более точно измерить MS _W.. Представьте, например, что зависимая переменная в исследовании — это мера времени реакции. Некоторые участники будут быстрее или медленнее других из-за устойчивых индивидуальных различий в их нервной системе, мышцах и других факторах. В плане между субъектами эти стабильные индивидуальные различия просто увеличат изменчивость внутри групп и увеличат значение MS _W . Однако при внутрисубъектном плане эти стабильные индивидуальные различия можно измерить и вычесть из значения MS _W . Это более низкое значение MS _W означает более высокое значение F и более чувствительный тест.

Факторный анализ

Когда в факторный план включено более одной независимой переменной, подходящим подходом является факторный дисперсионный анализ . Опять же, основы факторного дисперсионного анализа такие же, как и для однофакторного дисперсионного анализа и дисперсионного анализа с повторными измерениями. Основное отличие состоит в том, что для каждого основного эффекта и для каждого взаимодействия выводятся коэффициент F и значение p . Возвращаясь к нашему примеру с оценкой калорий, представьте, что психолог по вопросам здоровья проверяет влияние основного участника (психология или питание) и типа пищи (печенье или гамбургер) в факторном плане. Факторный ANOVA даст отдельные отношения F и pзначения для основного эффекта мажора, основного эффекта типа пищи и взаимодействия между мажором и едой. Соответствующие модификации должны быть сделаны в зависимости от того, является ли дизайн между субъектами, внутри субъектов или смешанными.

Тестирование Пирсона r

Для взаимосвязей между количественными переменными, где r Пирсона используется для описания силы этих взаимосвязей, подходящей проверкой нулевой гипотезы является проверка r Пирсона . Основная логика точно такая же, как и для других тестов нулевой гипотезы. В этом случае нулевая гипотеза состоит в том, что в популяции нет связи. Мы можем использовать греческую строчную букву rho (ρ) для представления соответствующего параметра: ρ = 0. Альтернативная гипотеза состоит в том, что в популяции существует взаимосвязь: ρ ≠ 0. Как и в случае t - теста, этот тест может быть двусторонним . если у исследователя нет ожиданий в отношении направления связи или односторонние, если исследователь ожидает, что отношения будут развиваться в определенном направлении.

Можно использовать r Пирсона для выборки, чтобы вычислить t - показатель с N - 2 степенями свободы, а затем продолжить, как для t - критерия. Однако из-за того, как он вычисляется, r Пирсона также можно рассматривать как собственную тестовую статистику. Статистические онлайн-инструменты и статистическое программное обеспечение, такое как Excel и SPSS, обычно вычисляют r Пирсона и предоставляют значение p , связанное с этим значением r Пирсона . Как всегда, если значение р меньше 0,05, мы отклоняем нулевую гипотезу и делаем вывод, что существует связь между переменными в популяции. Если рзначение больше 0,05, мы сохраняем нулевую гипотезу и делаем вывод, что недостаточно доказательств, чтобы сказать, что существует связь в популяции. Если мы вычислим r Пирсона вручную, мы можем использовать таблицу, подобную Таблице 13.5 «Таблица критических значений Пирсона» , которая показывает критические значения r для различных размеров выборок, когда α равно 0,05. Выборочное значение r Пирсона, превышающее критическое значение, является статистически значимым.

Таблица 13.5 Таблица критических значений r Пирсона при α = 0,05

	Критическое значение r
Н	Однохвостый	Двухвостый
5	0,805	0,878
10	0,549	0,632
15	.441	0,514
20	0,378	0,444
25	0,337	0,396
30	.306	0,361
35	0,283	0,334
40	0,264	.312
45	0,248	0,294
50	0,235	0,279
55	0,224	0,266
60	0,214	0,254
65	.206	0,244
70	.198	0,235
75	.191	0,227
80	0,185	.220
85	.180	0,213
90	0,174	.207
95	.170	.202
100	0,165	.197

Пример теста Пирсона r

Представьте, что психолога здоровья интересует корреляция между оценками калорийности людей и их весом. У него нет ожиданий относительно направления отношений, поэтому он решает провести двусторонний тест. Он вычисляет корреляцию для выборки из 22 студентов колледжа и находит, что r Пирсона составляет -0,21. Статистическое программное обеспечение, которое он использует, сообщает ему, что значение р равно 0,348. Это больше, чем 0,05, поэтому он сохраняет нулевую гипотезу и заключает, что нет никакой связи между оценками калорий людей и их весом. Если бы ему нужно было вычислить r Пирсона вручную, он мог бы взглянуть на таблицу 13.5 «Таблица критических значений Пирсона».и видим, что критическое значение для 22 - 2 = 20 степеней свободы составляет 0,444. Тот факт, что r Пирсона для выборки менее экстремально, чем это критическое значение, говорит ему, что значение p больше 0,05 и что он должен сохранить нулевую гипотезу.

КЛЮЧЕВЫЕ ВЫВОДЫ

• Чтобы сравнить два средних значения, наиболее распространенным тестом нулевой гипотезы является t - тест. Одновыборочный t - критерий используется для сравнения среднего значения одной выборки с интересующим гипотетическим средним значением генеральной совокупности, t - критерий зависимых выборок используется для сравнения двух средних в планах внутри субъектов, а t - критерий независимых выборок используется для сравнить два средства в дизайне между субъектами.
• Для сравнения более чем двух средних наиболее распространенным тестом нулевой гипотезы является дисперсионный анализ (ANOVA). Однофакторный дисперсионный анализ используется для планов между субъектами с одной независимой переменной, дисперсионный анализ с повторными измерениями используется для внутрисубъектных планов, а факторный дисперсионный анализ используется для факторных планов.
• Проверка нулевой гипотезы r Пирсона используется для сравнения выборочного значения r Пирсона с гипотетическим значением генеральной совокупности, равным 0.

УПРАЖНЕНИЯ

1. Практика: используйте один из онлайн-инструментов, Excel или SPSS, чтобы воспроизвести t-критерий для одной выборки , t - критерий для зависимых выборок , t - критерий для независимых выборок и однофакторный дисперсионный анализ для четырех наборов данных оценки калорий, представленных в этом документе. раздел.
2. Практика: Выборка из 25 студентов колледжа оценила свое дружелюбие по шкале от 1 ( намного ниже среднего ) до 7 ( намного выше среднего ). Их средний рейтинг составил 5,30 при стандартном отклонении 1,50. Проведите одновыборочный t - критерий, сравнивая их средний рейтинг с гипотетическим средним рейтингом 4 ( среднее ). Вопрос в том, склонны ли студенты колледжей оценивать себя как более дружелюбных, чем в среднем.
3. Практика: Решите, является ли каждое из следующих значений r Пирсона статистически значимым как для одностороннего, так и для двустороннего критерия. (а) Корреляция между ростом и IQ составляет +,13 в выборке из 35 человек. (б) Для выборки из 88 студентов колледжа корреляция между тем, насколько они отвращение испытывают, и резкостью их моральных суждений составляет +,23. (c) Корреляция между количеством ежедневных хлопот и хорошим настроением составляет -0,43 для выборки из 30 взрослых среднего возраста.

13.3 Дополнительные соображения

ЦЕЛИ ОБУЧЕНИЯ

1. Дайте определение ошибкам Типа I и Типа II, объясните, почему они происходят, и определите некоторые шаги, которые можно предпринять, чтобы свести к минимуму их вероятность.
2. Дайте определение статистической мощности, объясните ее роль в планировании новых исследований и используйте онлайн-инструменты для расчета статистической мощности простых планов исследований.
3. Перечислите некоторые критические замечания по поводу традиционной проверки нулевых гипотез, а также некоторые способы борьбы с этими критическими замечаниями.

В этом разделе мы рассмотрим несколько других вопросов, связанных с проверкой нулевой гипотезы, включая те, которые полезны при планировании исследований и интерпретации результатов. Мы даже рассматриваем некоторые давние критические замечания в отношении проверки нулевых гипотез, а также некоторые шаги, предпринятые исследователями в области психологии для их устранения.

Ошибки при проверке нулевой гипотезы

При проверке нулевой гипотезы исследователь пытается сделать разумный вывод о совокупности на основе выборки. К сожалению, правильность этого вывода не гарантируется. Это показано на рис. 13.3 «Два типа правильных решений и два типа ошибок при проверке нулевой гипотезы».. Строки этой таблицы представляют два возможных решения, которые мы можем принять при проверке нулевой гипотезы: отклонить или сохранить нулевую гипотезу. Столбцы представляют два возможных состояния мира: нулевая гипотеза ложна или верна. Таким образом, четыре ячейки таблицы представляют четыре различных результата проверки нулевой гипотезы. Два исхода — отклонение нулевой гипотезы, когда она ложна, и сохранение ее, когда она верна, — являются правильными решениями. Два других — отклонение нулевой гипотезы, когда она верна, и сохранение ее, когда она ложна, — являются ошибками.

Рис. 13.3 . Два типа правильных решений и два типа ошибок при проверке нулевой гипотезы

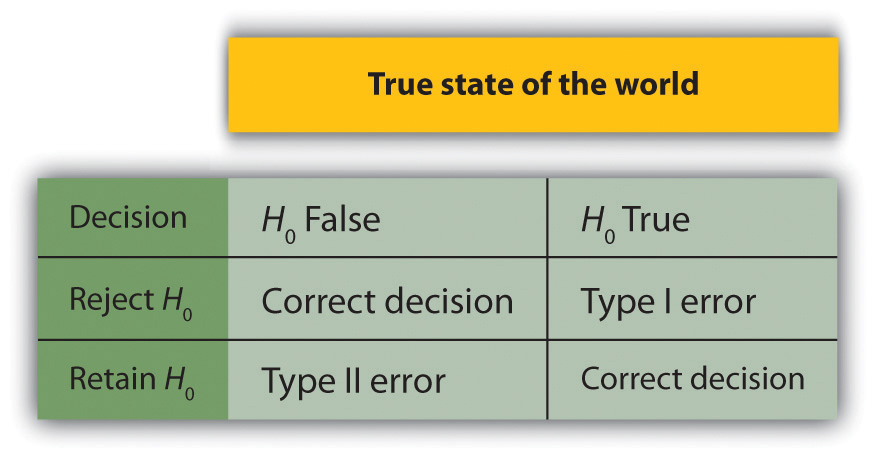
Отказ от нулевой гипотезы, когда она верна, называется ошибкой первого рода . Это означает, что мы пришли к выводу, что в популяции есть связь, хотя на самом деле ее нет. Ошибки типа I возникают потому, что даже при отсутствии взаимосвязи в генеральной совокупности ошибка выборки сама по себе иногда приводит к экстремальным результатам. На самом деле, когда нулевая гипотеза верна и α равно 0,05, мы ошибочно отвергаем нулевую гипотезу в 5% случаев. (Вот почему α иногда называют «коэффициентом ошибок типа I».) Сохранение нулевой гипотезы, когда она ложна, называется ошибкой типа II .. Это означает, что мы пришли к выводу, что родства в популяции нет, хотя на самом деле оно есть. На практике ошибки типа II возникают главным образом из-за того, что плану исследования не хватает достаточной статистической мощности для выявления взаимосвязи (например, выборка слишком мала). Вскоре мы еще поговорим о статистической мощности.

В принципе, можно уменьшить вероятность ошибки типа I, установив значение α меньше 0,05. Установка его на 0,01, например, будет означать, что если нулевая гипотеза верна, то вероятность ее ошибочного отклонения составляет всего 1%. Но усложнение процесса отклонения истинных нулевых гипотез также затрудняет отклонение ложных и, следовательно, увеличивает вероятность ошибки типа II. Точно так же можно уменьшить вероятность ошибки типа II, установив α чем-то большим, чем 0,05 (например, 0,10). Но облегчение отклонения ложных нулевых гипотез также облегчает отклонение истинных и, следовательно, увеличивает вероятность ошибки типа I. Это дает некоторое представление о том, почему принято устанавливать α равным 0,05.

Возможность совершения ошибок типа I и типа II имеет несколько важных последствий для интерпретации результатов наших собственных и чужих исследований. Во-первых, нам следует с осторожностью интерпретировать результаты любого отдельного исследования, потому что есть шанс, что оно отражает ошибку типа I или типа II. Вот почему исследователи считают важным повторить свои исследования. Каждый раз, когда исследователи повторяют исследование и находят похожий результат, они по праву становятся более уверенными в том, что результат представляет собой реальное явление, а не просто ошибку типа I или типа II.

Еще одна проблема, связанная с ошибками типа I, — это так называемая проблема ящика для файлов (Rosenthal, 1979). Розенталь, Р. (1979). Проблема с ящиком для файлов и терпимость к нулевым результатам. Психологический бюллетень , 83 , 638–641.Идея состоит в том, что, когда исследователи получают статистически значимые результаты, они, как правило, представляют их для публикации, а редакторы журналов и рецензенты склонны их принимать. Но когда исследователи получают незначительные результаты, они, как правило, не представляют их для публикации, а если и представляют, то редакторы журналов и рецензенты, как правило, их не принимают. Исследователи заканчивают тем, что прячут эти несущественные результаты в ящик для документов (или в настоящее время в папку на своем жестком диске). Одним из следствий этого является то, что опубликованная литература, вероятно, содержит более высокую долю ошибок типа I, чем мы могли бы ожидать, основываясь только на статистических соображениях. Даже когда между двумя переменными в популяции существует взаимосвязь, опубликованная исследовательская литература, вероятно, преувеличивает силу этой взаимосвязи. Представьте, например, что связь между двумя переменными в совокупности положительна, но слаба (например, ρ = +,10). Если несколько исследователей проводят исследования этой взаимосвязи, ошибка выборки, вероятно, приведет к результатам, варьирующимся от слабых отрицательных взаимосвязей (например,r = −0,10) до умеренно сильных положительных (например, r = +0,40). Но из-за проблемы ящика с файлами, скорее всего, будут опубликованы только те исследования, которые показывают положительные отношения от умеренных до сильных. В результате эффект, о котором сообщается в опубликованной литературе, имеет тенденцию быть сильнее, чем на самом деле в популяции.

Проблема ящика с папками трудна, потому что она является продуктом того, как научные исследования традиционно проводились и публиковались. Одно из решений может состоять в том, чтобы редакторы журналов и рецензенты оценивали исследования, представленные для публикации, не зная результатов этого исследования. Идея состоит в том, что если вопрос исследования признан интересным, а метод признан надежным, то незначительный результат должен быть столь же важным и достойным публикации, как и значительный. За исключением столь радикального изменения в том, как исследование оценивается для публикации, исследователи все еще могут приложить усилия, чтобы сохранить свои незначительные результаты и поделиться ими как можно шире (например, на профессиональных конференциях). Многие научные дисциплины теперь имеют журналы, посвященные публикации несущественных результатов. В психологии, например,Журнал статей в поддержку нулевой гипотезы ( http://www.jasnh.com ).

Статистическая мощность

Статистическая мощность плана исследования — это вероятность отклонения нулевой гипотезы с учетом размера выборки и ожидаемой силы взаимосвязи. Например, статистическая мощность исследования с 50 участниками и ожидаемым коэффициентом Пирсона rиз +0,30 в населении составляет 0,59. То есть вероятность отклонения нулевой гипотезы составляет 59%, если корреляция населения действительно составляет +0,30. Статистическая мощность является дополнением к вероятности совершения ошибки второго рода. Таким образом, в этом примере вероятность совершения ошибки типа II будет равна 1 - 0,59 = 0,41. Ясно, что исследователи должны быть заинтересованы в эффективности своих исследовательских планов, если они хотят избежать ошибок типа II. В частности, они должны убедиться, что их дизайн исследования имеет достаточную мощность, прежде чем собирать данные. Общепринятым правилом является то, что степень 0,80 является адекватной. Это означает, что вероятность отклонения нулевой гипотезы для ожидаемой силы связи составляет 80%.

Тема расчета мощности для различных исследовательских планов и проверки нулевых гипотез выходит за рамки этой книги. Однако существуют онлайн-инструменты, которые позволяют вам сделать это, введя размер выборки, ожидаемую силу связи и уровень α для различных проверок гипотез (см. «Вычислительная мощность в Интернете»). Кроме того, в таблице 13.6 «Размеры выборки, необходимые для достижения статистической мощности 0,80 для различных ожидаемых сил связи для независимых выборок» показан размер выборки, необходимый для достижения мощности 0,80 для слабых, средних и сильных связей для двух независимых выборок. -критерий t для независимых выборок и двусторонний критерий Пирсона r. Обратите внимание, что в этой таблице усиливается мнение, сделанное ранее о силе взаимосвязи, размере выборки и статистической значимости. В частности, слабые отношения требуют очень больших выборок для обеспечения адекватной статистической мощности.

Таблица 13.6 Размер выборки, необходимый для достижения статистической мощности 0,80 для различных ожидаемых сил связи для теста t независимых выборок и теста Пирсона r

Проверка нулевой гипотезы
Сила отношений	t - критерий независимых выборок	Тест Пирсона r
Сильный ( d = 0,80, r = 0,50)	52	28
Средний ( d = 0,50, r = 0,30)	128	84
Слабый ( d = 0,20, r = 0,10)	788	782

Что делать, если вы обнаружите, что ваш план исследования не обладает достаточной мощностью? Представьте, например, что вы проводите эксперимент между субъектами с 20 участниками в каждом из двух условий и ожидаете среднюю разницу ( d = 0,50) в популяции. Статистическая мощность этого плана составляет всего 0,34. То есть, даже если имеется среднее различие в популяции, вероятность отклонения нулевой гипотезы составляет примерно один к трем, а вероятность совершения ошибки типа II составляет примерно два из трех. Учитывая время и усилия, затраченные на проведение исследования, это, вероятно, кажется неприемлемо низким шансом отвергнуть нулевую гипотезу и неприемлемо высоким шансом совершения ошибки типа II.

Учитывая, что статистическая мощность зависит в первую очередь от силы связи и размера выборки, есть два основных шага, которые вы можете предпринять, чтобы увеличить статистическую мощность: увеличить силу связи или увеличить размер выборки. Повышение силы взаимосвязи иногда может быть достигнуто за счет более жесткой манипуляции или более тщательного контроля посторонних переменных для уменьшения количества шума в данных (например, путем использования плана внутри субъектов, а не плана между субъектами). Однако обычной стратегией является увеличение размера выборки. Для любой ожидаемой силы связи всегда будет некоторая выборка, достаточно большая для достижения адекватной мощности.

Вычислительная мощность онлайн

Следующие ссылки относятся к инструментам, позволяющим вычислять статистическую мощность для различных планов исследований и проверок нулевых гипотез путем ввода информации об ожидаемой силе взаимосвязи, размере выборки и уровне α. Они также позволяют вычислить размер выборки, необходимый для достижения желаемого уровня мощности (например, 0,80). Во-первых, это онлайн-инструмент. Вторая — бесплатная загружаемая программа под названием G*Power.

• Страница силы и размера выборки Расса Лента: http://www.stat.uiowa.edu/~rlenth/Power/index.html
• G*Power: http://www.psycho.uni-duesseldorf.de/aap/projects/gpower

Проблемы с проверкой нулевой гипотезы и некоторые решения

Опять же, проверка нулевой гипотезы является наиболее распространенным подходом к статистике вывода в психологии. Однако не обошлось без критиков. Фактически, в последние годы критика стала настолько заметной, что Американская психологическая ассоциация созвала целевую группу, чтобы дать рекомендации о том, как с ней бороться (Wilkinson & Task Force on Statistical Inference, 1999). Уилкинсон Л. и Целевая группа по статистическим выводам. (1999). Статистические методы в журналах по психологии: рекомендации и пояснения. Американский психолог , 54 , 594–604. В этом разделе мы рассмотрим некоторые критические замечания и некоторые рекомендации.

Критика проверки нулевой гипотезы

Некоторая критика проверки нулевой гипотезы сосредоточена на неправильном понимании ее исследователями. Мы уже видели, например, что значение p часто неправильно интерпретируется как вероятность того, что нулевая гипотеза верна. (Напомним, что на самом деле это вероятность результата выборки , если нулевая гипотеза верна.) Тесно связанное неправильное толкование состоит в том, что 1 - p - это вероятность воспроизведения статистически значимого результата. В одном исследовании 60 % выборки профессиональных исследователей считали, что значение p , равное 0,01, — для независимого t - критерия с 20 участниками в каждой — означает 99-процентную вероятность воспроизвести статистически значимый результат (Оукс). , 1986).Оукс, М. (1986). Статистический вывод: комментарий для социальных и поведенческих наук . Чичестер, Великобритания: Wiley. Наше предыдущее обсуждение власти должно прояснить, что это слишком оптимистично. Как показывает таблица 13.5 «Таблица критических значений Пирсона» , даже если бы существовала большая разница между средними значениями в популяции, для достижения степени 0,80 потребовалось бы 26 участников на выборку. А программа G*Power показывает, что для достижения степени 0,99 потребуется 59 участников на выборку.

Другой набор критических замечаний касается логики проверки нулевой гипотезы. Для многих строгое правило отвергать нулевую гипотезу, когда p меньше 0,05, и сохранять ее, когда p больше 0,05, не имеет большого смысла. Эта критика связана не с конкретным значением 0,05, а с идеей о том, что должна быть какая-то жесткая разделительная линия между результатами, которые считаются значимыми, и результатами, которые не являются таковыми. Представьте себе два исследования одной и той же статистической взаимосвязи с одинаковыми размерами выборки. Один имеет значение p 0,04, а другой - pзначение 0,06. Хотя оба исследования дали по существу один и тот же результат, первое, вероятно, будет сочтено интересным и достойным публикации, а второе просто не имеет большого значения. Это соглашение, вероятно, помешает публикации хороших исследований и усугубит проблему ящика для документов.

Еще одна группа критических замечаний сосредоточена на идее о том, что проверка нулевой гипотезы — даже при правильном понимании и проведении — просто не очень информативна. Напомним, что нулевая гипотеза состоит в том, что между переменными в генеральной совокупности нет связи (например, d Коэна или r Пирсона точно равны 0). Таким образом, отвергнуть нулевую гипотезу — значит просто сказать, что в популяции существует некоторая ненулевая взаимосвязь. Но на самом деле это не очень много говорит. Представьте, если бы химия могла сказать нам только то, чтовзаимосвязь между температурой газа и его объемом, а не предоставление точного уравнения для описания этой взаимосвязи. Некоторые критики даже утверждают, что отношение между двумя переменными в генеральной совокупности никогда не бывает точно равным 0, если оно проводится с достаточным количеством знаков после запятой. Другими словами, нулевая гипотеза никогда не бывает истинна буквально. Таким образом, отказ от него не говорит нам ничего, чего мы еще не знали!

Справедливости ради следует отметить, что многие исследователи встали на защиту проверки нулевой гипотезы. Один из них, Роберт Абельсон, утверждал, что при правильном понимании и проведении проверка нулевой гипотезы действительно служит важной цели (Abelson, 1995). Абельсон, Р.П. (1995). Статистика как принципиальный аргумент . Махва, Нью-Джерси: Эрлбаум. Особенно когда речь идет о новых явлениях, это дает исследователям принципиальный способ убедить других в том, что их результаты не следует отбрасывать как простое случайное происшествие.

Что делать?

Даже те, кто защищает проверку нулевой гипотезы, признают многие связанные с этим проблемы. Но что делать? Некоторые предложения теперь появляются в Руководстве по публикации . Во-первых, каждый тест нулевой гипотезы должен сопровождаться показателем размера эффекта, таким как d Коэна или r Пирсона . Поступая таким образом, исследователь дает оценку того, насколько сильны отношения в популяции, а не только есть ли они или нет. (Помните, что значение p не может служить мерой силы связи, поскольку оно также зависит от размера выборки. Даже очень слабый результат может быть статистически значимым, если выборка достаточно велика.)

Другое предложение состоит в том, чтобы использовать доверительные интервалы, а не тесты на нулевую гипотезу. Доверительный интервалвокруг статистики - это диапазон значений, который рассчитывается таким образом, что некоторый процент времени (обычно 95%) параметр совокупности будет находиться в этом диапазоне. Например, выборка из 20 студентов колледжа может иметь оценку средней калорийности шоколадного печенья, равную 200, с 95% доверительным интервалом от 160 до 240. Население студентов колледжей составляет от 160 до 240 человек. Сторонники доверительных интервалов утверждают, что их гораздо легче интерпретировать, чем тесты нулевой гипотезы. Еще одно преимущество доверительных интервалов заключается в том, что они предоставляют информацию, необходимую для проверки нулевой гипотезы, если кто-то захочет. В этом примере выборочное среднее значение 200 значительно отличается на уровне . 05 из любой гипотетической популяции означает, что лежит за пределами доверительного интервала. Таким образом, доверительный интервал от 160 до 240 говорит нам о том, что среднее значение выборки статистически значимо отличается от гипотетического среднего значения популяции, равного 250.

Наконец, существуют более радикальные решения проблем проверки нулевой гипотезы, которые включают использование совершенно разных подходов к статистике логического вывода. Байесовская статистика , например, представляет собой подход, при котором исследователь указывает вероятность того, что нулевая гипотеза и любые важные альтернативные гипотезы верны, прежде чем проводить исследование, проводит исследование, а затем обновляет вероятности на основе данных. Пока рано говорить о том, станет ли этот подход общепринятым в психологических исследованиях. На данный момент проверка нулевой гипотезы, подкрепленная мерами размера эффекта и доверительными интервалами, остается доминирующим подходом.

КЛЮЧЕВЫЕ ВЫВОДЫ

• Решение отклонить или сохранить нулевую гипотезу не обязательно будет правильным. Ошибка типа I возникает, когда нулевая гипотеза отвергается, когда она верна. Ошибка типа II возникает, когда не удается отвергнуть нулевую гипотезу, когда она ложна.
• Статистическая мощность плана исследования — это вероятность отклонения нулевой гипотезы с учетом ожидаемой силы взаимосвязи в популяции и размера выборки. Исследователи должны убедиться, что их исследования имеют достаточную статистическую мощность, прежде чем проводить их.
• Проверка нулевой гипотезы подвергалась критике на том основании, что исследователи неправильно ее понимают, что она нелогична и неинформативна. Другие утверждают, что он служит важной цели, особенно при использовании с мерами размера эффекта, доверительными интервалами и другими методами. Он остается доминирующим подходом к логической статистике в психологии.

УПРАЖНЕНИЯ

1. Обсуждение: Исследователь сравнивает эффективность двух форм психотерапии социальной фобии, используя t - тест независимых выборок.

   1. Объясните, что для исследователя будет означать совершение ошибки первого рода.
   2. Объясните, что для исследователя будет означать совершение ошибки типа II.
2. Обсуждение: представьте, что вы проводите t -тест, и значение p равно 0,02. Как бы вы объяснили, что означает это значение p , тому, кто еще не знаком с проверкой нулевой гипотезы? Обязательно избегайте распространенных неверных интерпретаций значения p .